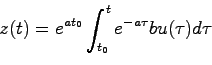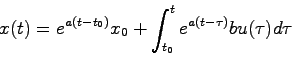: 遷移行列の算出
: sysconh16
: 状態変数と状態方程式
前節のように状態方程式は一般にベクトル変数の1階微分方程式(1階行列微分方程式)になり、古典制御のように入力と出力の関係を導くためにはこの状態方程式を解く必要がある。
ここではまず1階行列微分方程式としての状態方程式を仮に1変数(スカラー)の1階微分方程式とした場合にその解がどのようにして求められるか。また、同様の方法でベクトル変数の状態方程式を解くにはどのようにすればよいかについて述べる。
次の1階微分方程式を考える.ただし,変数はすべてスカラーであるとする.
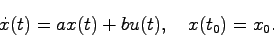 |
(2.1) |
この方程式は一般的な常微分方程式であり定数変化法やラプラス変換を用いる解法により
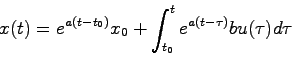 |
(2.2) |
と解くことができる。
このことから1階行列微分方程式
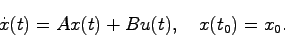 |
(2.3) |
についても同様の解
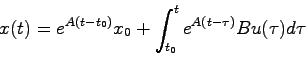 |
(2.4) |
が得られることが望ましい。ただし、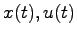 はそれぞれ
はそれぞれ 次,
次,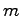 次ベクトル、
次ベクトル、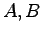 は
は
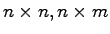 行列である。
行列である。
(2.4)式は一見すると変数がベクトルであることを除けば何の変哲もない式に思える。しかし指数関数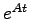 を見ると、指数部が行列であり具体的なイメージが掴めないであろう。そこで、状態方程式(2.3)の解が(2.4)になることも含め通常の指数関数
を見ると、指数部が行列であり具体的なイメージが掴めないであろう。そこで、状態方程式(2.3)の解が(2.4)になることも含め通常の指数関数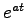 について復習する。
について復習する。
指数関数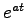 は次の無限級数で定義される:
は次の無限級数で定義される:
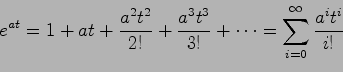 |
(2.5) |
また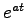 の性質として
の性質として
が挙げられる。実際これらの性質は微分方程式(2.1)から、その解(2.2)を求める場合にも利用される。
このことから指数部が行列 の場合にも同様の定義で、同様の性質が成り立てば都合がよいであろう。そのため任意の行列
の場合にも同様の定義で、同様の性質が成り立てば都合がよいであろう。そのため任意の行列 に対して
に対して
と定義できるための条件を考えてみる。明らかに、上式を見るといくつが確認すべき点があるのでまずそれらを列挙する。
- 上式で
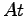 は行列であるから右辺第一項の
は行列であるから右辺第一項の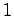 も行列とする必要がある。
も行列とする必要がある。
- 上式で
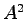 が計算できるためには行列
が計算できるためには行列 が正方行列でなければならない。
が正方行列でなければならない。
- 上式は行列の無限級数による表現であるが、これが意味を持つには無限級数が収束する必要がある。
これらのうち初めの2つは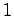 を単位行列
を単位行列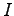 、
、 を
を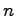 次正方行列に限定すればよい。3番目は本講義の範囲を超えるので省略するが、これも
次正方行列に限定すればよい。3番目は本講義の範囲を超えるので省略するが、これも が
が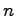 次正方行列であれば特に問題ない。
次正方行列であれば特に問題ない。
以上のことから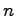 次正方行列
次正方行列 に対する(行列)指数関数
に対する(行列)指数関数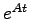 を、とりあえず、次式で定義する:
を、とりあえず、次式で定義する:
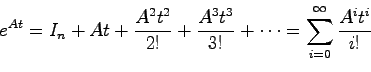 |
(2.6) |
この定義がスカラーの場合の拡張になっているかを調べるためには、スカラー同様次の性質が成り立つかを調べればよい。
以下、これについて証明する。ただし、(2.7)式,(2.10)式は(2.6)式の定義より明らかなので省略する。
- (2.8)式について:
ここで二項定理を利用した。
- (2.9)式について:
(2.8)式において
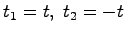 と置くと
と置くと
したがって、左から
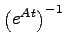 を作用させれば(2.10)式が得られる。
を作用させれば(2.10)式が得られる。
以上により(2.6)式により定義した、正方行列 の行列指数関数が通常の指数関数と同様の性質を持つことがわかった。次に(2.4)式で与えられる
の行列指数関数が通常の指数関数と同様の性質を持つことがわかった。次に(2.4)式で与えられる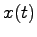 が本当に行列微分方程式(2.3)式の解であるかを確かめる。このため(2.4)式を
が本当に行列微分方程式(2.3)式の解であるかを確かめる。このため(2.4)式を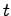 で微分する(右辺第2項は積の微分になることに注意)と
で微分する(右辺第2項は積の微分になることに注意)と
となる。これに(2.4)式を代入すれば(2.3)式が得られ、これにより(2.4)式が(2.3)式の解であることがわかった。
付録
(2.2)式の導出(定数変化法による)
(2.1)式において,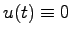 とおくと
とおくと
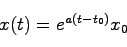 |
(2.11) |
となる.このことから(2.1)式の解は,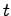 の関数
の関数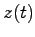 を用いて
を用いて
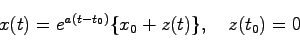 |
(2.12) |
となることが予想される.そこで,(2.12)式を(2.1)式に代入すると
となり,
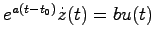 を得る.これより
を得る.これより
であるから,初期条件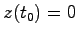 を考慮して積分すると
を考慮して積分すると
となり,(2.12)式へ代入すると
が得られる.



: 遷移行列の算出
: sysconh16
: 状態変数と状態方程式
endo
平成16年6月30日
![]() を見ると、指数部が行列であり具体的なイメージが掴めないであろう。そこで、状態方程式(2.3)の解が(2.4)になることも含め通常の指数関数
を見ると、指数部が行列であり具体的なイメージが掴めないであろう。そこで、状態方程式(2.3)の解が(2.4)になることも含め通常の指数関数![]() について復習する。
について復習する。
![]() は次の無限級数で定義される:
は次の無限級数で定義される:
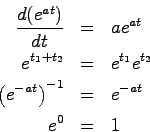
![]() の場合にも同様の定義で、同様の性質が成り立てば都合がよいであろう。そのため任意の行列
の場合にも同様の定義で、同様の性質が成り立てば都合がよいであろう。そのため任意の行列![]() に対して
に対して
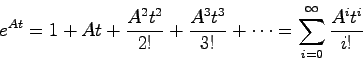
![]() 次正方行列
次正方行列![]() に対する(行列)指数関数
に対する(行列)指数関数![]() を、とりあえず、次式で定義する:
を、とりあえず、次式で定義する:
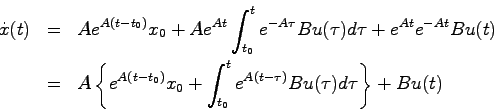
![]() とおくと
とおくと