


: 直和
: ベクトル空間
: ベクトル空間の定義
ベクトル空間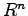 に属する有限個のベクトルの集合
に属する有限個のベクトルの集合
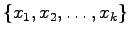 に対して,適当なスカラー
に対して,適当なスカラー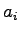 によって
によって
と表されるベクトル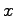 の集合
の集合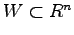 を考える.すると
を考える.すると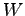 もまたベクトル空間になり,これをベクトルの集合
もまたベクトル空間になり,これをベクトルの集合
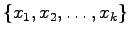 によって張られる
によって張られる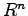 の部分空間と呼び
の部分空間と呼び
で表す.さらに
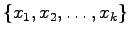 が一次独立であるとき,すなわち
が一次独立であるとき,すなわち
となるスカラー
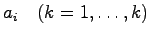 が
が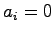 以外には存在しないならば,部分空間
以外には存在しないならば,部分空間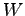 の次元は
の次元は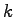 であるといい,ベクトルの
であるといい,ベクトルの
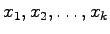 を
を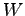 の基底と呼ぶ.ただし,空間
の基底と呼ぶ.ただし,空間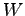 の基底は一意でないことに注意!
の基底は一意でないことに注意!
例 次のような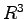 の部分空間
の部分空間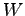 を考える.
を考える.
この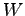 の基底は明らかに
の基底は明らかに
![$\left[ \begin{array}{ccc} 1 & 0 & 0 \end{array}\right]^T$](img453.png) と
と
![$\left[ \begin{array}{ccc} 0 & 1 & 0 \end{array}\right]^T$](img454.png) であるが,別の基底
であるが,別の基底
を考えることもできる.
endo
平成16年6月30日
![]() の部分空間
の部分空間![]() を考える.
を考える.
![\begin{displaymath}
W = {\rm span}\{ \left[ \begin{array}{ccc} 1 & 0 & 0 \end{ar...
...T,
\left[ \begin{array}{ccc} 0 & 1 & 0 \end{array}\right]^T\}.
\end{displaymath}](img452.png)
![$\left[ \begin{array}{ccc} 1 & 0 & 0 \end{array}\right]^T$](img453.png) と
と
![$\left[ \begin{array}{ccc} 0 & 1 & 0 \end{array}\right]^T$](img454.png) であるが,別の基底
であるが,別の基底
![\begin{displaymath}
\left[ \begin{array}{ccc} 1 & 0 & 0 \end{array}\right]^T,\quad
\left[ \begin{array}{ccc} 1 & 1 & 0 \end{array}\right]^T
\end{displaymath}](img455.png)