


: 正準変換
: ベクトル空間
: 直和
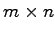 実行列
実行列 によって定まるベクトル空間
によって定まるベクトル空間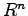 からベクトル空間
からベクトル空間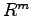 への変換
への変換
を考えると
が成立する.上式を変換 の線形性と呼び,線形性の成り立つ変換を線形変換と呼ぶ.
の線形性と呼び,線形性の成り立つ変換を線形変換と呼ぶ.
任意の線形変換 に対して
に対して
で表される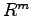 の部分空間
の部分空間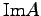 を変換
を変換 の値域という(
の値域という(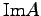 が部分空間になるかは各自検証).また
が部分空間になるかは各自検証).また
で表される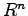 の部分空間
の部分空間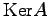 を変換
を変換 の零空間という(
の零空間という(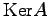 が部分空間になるかは各自検証).
が部分空間になるかは各自検証).
特に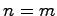 の場合には
の場合には
が成立する.すなわちベクトル空間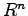 を,
を, に関連した2つの部分空間の直和として表すことができる.
に関連した2つの部分空間の直和として表すことができる.
例 次の線形変換を考える:
これに対し値域,零空間は次のように求められる:
で与えられる.
endo
平成16年6月30日
![]() に対して
に対して
![]() の場合には
の場合には
![\begin{displaymath}
A = \left[ \begin{array}{ccc} 1 & 2 & 0 2 & 4 & 0 0 & 0 & 1 \end{array}\right]
\end{displaymath}](img475.png)
![\begin{eqnarray*}
{\rm Im}A &=& {\rm span}\{ \left[ \begin{array}{ccc} 1 & 2 & 0...
...}\{ \left[ \begin{array}{ccc} 2 & -1 & 0 \end{array}\right]^T
\}
\end{eqnarray*}](img476.png)