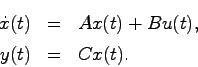
まず,正準変換を求める前に,可制御でないシステムを可制御なサブシステムと可制御でないサブシステムに分けることを考える.
議論 次の線形システムを考える:
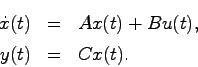
また,このことは,可制御な初期状態![]() の集合を
の集合を![]() と表したとき
と表したとき
システム![]() は可制御でないから明らかに
は可制御でないから明らかに
![]() である.
すなわち,線形空間
である.
すなわち,線形空間![]() の次元は
の次元は![]() であるから,
であるから,![]() 個の基底
個の基底
![]() が選べる.さらに
が選べる.さらに![]() 個の一次独立な列ベクトル
個の一次独立な列ベクトル
![]() を選び,
を選び,
![]() と一緒になって
と一緒になって![]() 次元空間の基底となっているものとする.
次元空間の基底となっているものとする.
これから次の変換行列![]() を考える:
を考える:
![\begin{displaymath}
T^{-1} = \left[ \begin{array}{cc} T_1 & T_2 \end{array}\right].
\end{displaymath}](img488.png)
![\begin{displaymath}
T_1 = \left[ \begin{array}{ccc} e_1 & \cdots & e_k \end{arra...
...[ \begin{array}{ccc} e_{k+1} & \cdots & e_n \end{array}\right]
\end{displaymath}](img489.png)
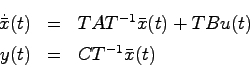
![\begin{displaymath}
T = \left[ \begin{array}{c} U_1 U_2 \end{array}\right]
\end{displaymath}](img492.png)
![\begin{displaymath}
TT^{-1} = \left[ \begin{array}{c}U_1 U_2 \end{array}\righ...
...t[ \begin{array}{cc} E_k & 0 0 & E_{n-k} \end{array}\right]
\end{displaymath}](img497.png)
ここで![]() は
は![]() 個の列ベクトル
個の列ベクトル
![]() から成り,これらによって可制御部分空間が張られる.したがって可制御部分空間内の任意のベクトル
から成り,これらによって可制御部分空間が張られる.したがって可制御部分空間内の任意のベクトル![]() は
は
また,
![$T^{-1} = \left[ \begin{array}{cc}T_1 & T_2\end{array}\right]$](img503.png) と
と
![$T = \left[ \begin{array}{c}U_1 U_2 \end{array}\right]$](img504.png) により
により
![\begin{eqnarray*}
\bar{A} &=& TAT^{-1} = \left[ \begin{array}{c}U_1 U_2 \end{...
...right]B =
\left[ \begin{array}{c}U_1B U_2B\end{array}\right]
\end{eqnarray*}](img505.png)
![]() の列はすべて可制御部分空間内にある.したがって
の列はすべて可制御部分空間内にある.したがって![]() のすべての列も可制御部分空間内にある.したがって
のすべての列も可制御部分空間内にある.したがって![]() から
から
![\begin{displaymath}
\dot{\bar{x}}(t) = \left[ \begin{array}{cc}
A_{11} & A_{12} ...
...}(t) +
\left[ \begin{array}{c}B_1 0 \end{array}\right] u(t)
\end{displaymath}](img510.png)
![]() による同値変換であるから,明らかに
による同値変換であるから,明らかに
![\begin{eqnarray*}
k &=& {\rm rank}M_C \\
&=& {\rm rank}\bar{M}_C \\
&=& {\rm r...
...B_1 & A_{11}^2B_1 & \cdots & A_{11}^{n-1}B_1
\end{array}\right].
\end{eqnarray*}](img512.png)
以上の議論により可制御でないシステムを可制御部分と可制御でない部分に分解することができる
次に,前述の説明で![]() の列がすべて可制御性部分空間内に入ることを述べたが,具体的には次のようにすればよい:
の列がすべて可制御性部分空間内に入ることを述べたが,具体的には次のようにすればよい:![]() を列ベクトル成分
を列ベクトル成分
![]() に分ける.すなわち
に分ける.すなわち
![\begin{displaymath}
B = \left[\begin{array}{cccc}b_1 & b_2 & \cdots & b_m \end{array}\right]
\end{displaymath}](img518.png)
![\begin{eqnarray*}
M_C &=& \left[ \begin{array}{cccc}B & AB & \cdots & A^{n-1}B \...
...m
\end{array}\right] & AB & \cdots & A^{n-1}B \end{array}\right]
\end{eqnarray*}](img519.png)
![\begin{displaymath}
\left[ \begin{array}{cccc} 1 & 0 & \cdots & 0
\end{array}\right]^T
\end{displaymath}](img521.png)
以下ではさらなる応用として正準分解を取り上げる.
定理 (カルマンの正準分解形)システム
![\begin{eqnarray*}
F &=& \left[ \begin{array}{cccc} F^{aa} & F^{ab} & F^{ac} & F^...
...& \left[ \begin{array}{cccc}0 & H^b & 0 & H^d \end{array}\right]
\end{eqnarray*}](img525.png)
![\begin{displaymath}
\left(\left[ \begin{array}{cc}
F^{aa} & F^{ab} \\
0 & F^{bb...
..., \left[ \begin{array}{c}
G^a G^b \end{array}\right]\right)
\end{displaymath}](img526.png)
![\begin{displaymath}
\left(\left[ \begin{array}{cc}
F^{bb} & F^{bd} \\
0 & F^{dd...
...],\left[ \begin{array}{cc}
H^b & H^d
\end{array}\right]\right)
\end{displaymath}](img527.png)
上記の定理の意味するところは,任意に与えられたシステムを4つのサブシステム
![]() に分解することができ,これら4つのサブシステムはそれぞれ
に分解することができ,これら4つのサブシステムはそれぞれ![]() は可制御不可観測,
は可制御不可観測,![]() は可制御可観測,
は可制御可観測,![]() は不可制御不可観測,
は不可制御不可観測,![]() は不可制御可観測なサブシステムである(図3.9参照).
は不可制御可観測なサブシステムである(図3.9参照).
定理の証明を行なう前に次の4つの補題を示す.
補題1
![]() を可制御部分空間とし,
を可制御部分空間とし,
![]() とする.なお,この
とする.なお,この![]() は
は![]() の定義から明らかなように,状態
の定義から明らかなように,状態![]() と区別がつかない状態
と区別がつかない状態![]() の集合であり,これを不可観測部分空間と呼ぶ.このとき
の集合であり,これを不可観測部分空間と呼ぶ.このとき
![]() は
は![]() についての不変部分空間になっている.すなわち
についての不変部分空間になっている.すなわち
![]() が成り立つ.
が成り立つ.
補題2 可制御部分空間![]() および不可観測部分空間
および不可観測部分空間
![]() より4つの部分空間
より4つの部分空間
![]() を次のように構成する
を次のように構成する
これらに対し次式が成り立つ:
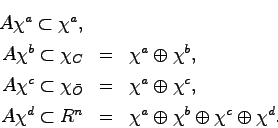
補題3 部分空間![]() から任意に選んだ一つの基底を
から任意に選んだ一つの基底を
![]() とし,これらを並べて得られる行列を
とし,これらを並べて得られる行列を![]() とする.他の部分空間に対しても同様に
とする.他の部分空間に対しても同様に
![]() を定める.すなわち
を定める.すなわち
![\begin{eqnarray*}
\Xi^a &:=& \left[ \begin{array}{ccc}\xi_1 & \ldots & \xi_{\mu_...
..._c+1} & \ldots & \xi_{\mu_a+\mu_b+\mu_c+\mu_d}\end{array}\right]
\end{eqnarray*}](img553.png)
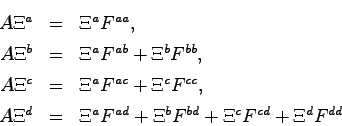
補題4 次式が成立する.
証明は一時的に省略する.
例3.10 システム
![\begin{displaymath}
A^2 = \left[ \begin{array}{cccc}
1 & 0 & 0 & 0 \\
2 & 1 & -...
... & 3 \\
0 & 0 & -1 & 0 \\
2 & 0 & -3 & -1
\end{array}\right]
\end{displaymath}](img560.png)
![\begin{displaymath}
M_C = \left[ \begin{array}{cccc}
-1 & -1 & -1 & -1 \\
1 & -...
...& 0 \\
1 & -1 & 1 & -1 \\
0 & 0 & 0 & 0
\end{array}\right]^T
\end{displaymath}](img561.png)
上の![]() から,
から,
![]() の基底がそれぞれ次のように求められる.
の基底がそれぞれ次のように求められる.
![]() の基底:
の基底:
![\begin{displaymath}
\left[ \begin{array}{cccc}1 & 0 & 0 & 1 \end{array}\right]^T...
...d
\left[ \begin{array}{cccc}0 & 1 & 0 & 0 \end{array}\right]^T
\end{displaymath}](img565.png)
![]() の基底:
の基底:
![\begin{displaymath}
\left[ \begin{array}{cccc}0 & 1 & 0 & 0 \end{array}\right]^T...
...
\left[ \begin{array}{cccc}0 & 0 & 0 & 1 \end{array}\right]^T.
\end{displaymath}](img566.png)
![\begin{displaymath}
\chi_C = {\rm span}\left\{
\left[ \begin{array}{c} 1 0 \...
... \begin{array}{c} 0 0 0 1 \end{array}\right]
\right\}
\end{displaymath}](img567.png)
![\begin{displaymath}
T^{-1} = \left[ \begin{array}{cccc}
0 & 1 & 0 & 0 \\
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 1 & 0
\end{array}\right]
\end{displaymath}](img575.png)
![\begin{eqnarray*}
F &=& TAT^{-1} = \left[ \begin{array}{cccc}
-1 & 1 & 1 & 0 ...
...-1} = \left[ \begin{array}{cccc}0 & 1 & 0 & 1 \end{array}\right]
\end{eqnarray*}](img576.png)
![\begin{displaymath}
\dot{\bar{x}} = \left[ \begin{array}{cccc}-1 & 1 & 1 & 0 ...
...t[ \begin{array}{cccc}0 & 1 & 0 & 1 \end{array}\right]
\bar{x}
\end{displaymath}](img577.png)