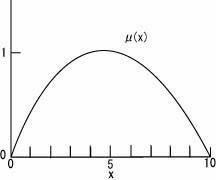
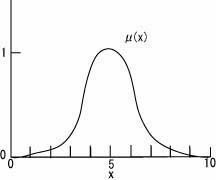
ファジィ集合の一例として「5ぐらい」という集合を考えてみます。この場合、「ぐらい」が示す範囲が曖昧なため、クリスプ集合では表現することができません。クリスプ集合では要素は集合に属するか、属さないかで完全に二分されるものでした。ファジィ集合では「要素が集合に完全に属する」、「・・・属する」、「・・・ほぼ属する」、「・・・おそらく属さない」、「・・・属さない」、「・・・完全に属さない」というように、要素がどの程度集合に属しているかを考えます。「5ぐらい」という集合では5は完全に属している事になり、4、6もほぼ属していると考えられます。この時、要素が完全に属しているなら1、完全に属していないなら0、ある度合いで属しているなら0〜1の適当値を与えて図示してみます。下図ではクリスプ集合の場合とは違って曖昧な範囲を取り扱えていることが分かります。こうして、ファジィ集合を用いることにより人間の曖昧な言葉をコンピュータで取り扱うことが可能になりました。

ファジィ集合ではある集合が与えられた場合、それを上図の様に表現することが可能です。その際に、要素が集合に属する度合いに応じて数値を与える関数をメンバシップ関数(μ(x))といい、その数値をメンバシップグレードといいます。ただし、ファジィ集合は主観的に定義されるため、メンバシップ関数は与える人によってその形状が異なります。下図も「5ぐらい」というファジィ集合を定義するメンバシップ関数です。