 |
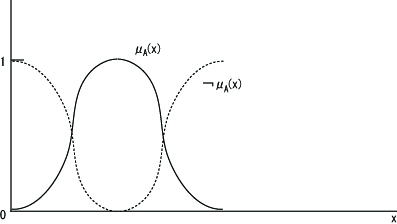
| 補集合 |
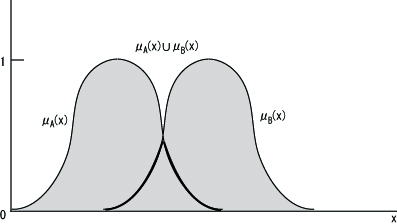 |
| 和集合 |
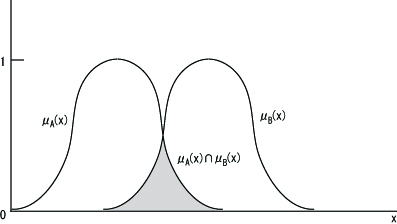 |
| 積集合 |
戻る 次へ
ファジィ集合の基本演算(2)
ファジィ集合の基本演算を数式で表すことを考えてみましょう。任意のファジィ集合をA、Bとし、それぞれのメンバシップ関数をμA(x)、μB(x)とすると、和集合、積集合、補集合は以下のように定義されます。
和集合:A∪B = μA(x)∨μB(x) (∨:max演算)
積集合:A∩B = μA(x)∧μB(x) (∧:min演算)
補集合:¬A = 1-μA(x)
また、二つのファジィ集合が等しいとは両者のメンバシップ関数が等しいことをいい、ファジ集合の包含関係はメンバシップ関数の大小関係で表さます。
包合関係:A=B ⇔ μA(x)=μB(x)
大小関係:A⊂B ⇔ μA(x)≦μB(x)