一般的に「もの」と「もの」との間は曖昧さを含む関係で成り立っています。例えば、「AとBは似ている」とか「整数100は整数3よりとても大きい」などは「似ている」、「とても大きい」が曖昧な関係に相当します。日常生活で用いる関係というのは、このような曖昧さを含む関係が多いわけですが、数学で用いられる関係とは、「AとBは等しい」、「整数100は整数3より大きい」というようにはっきりとした関係を指します。ファジィ関係とは、こうした数学で用いられている関係にファジィ集合の概念を導入し、それによって曖昧さを含む関係を表現しようというものです。
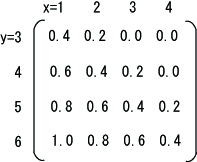
今、整数の集合X={1,2,3,4}、Y={3,4,5,6}に対して、「yはxより幾分大きい」という曖昧な関係が成り立っていたとします。これをファジィ関係を用いて表現することを考えます。ファジィ関係はファジィ集合によって定められており、そのメンバシップ関数とは関係が満たされている度合いを0〜1までの数値で与えるものです。この例では、(x=1,y=6)ではxに比べてyは充分に大きいため、メンバシップグレードは1.0となり、(x=4,y=3)ではxよりもyが小さいため、メンバシップグレードは0となります。それぞれのメンバシップグレードを行列で表現すると以下のようになります。
戻る 次へ