マムダニのファジィ推論（2）

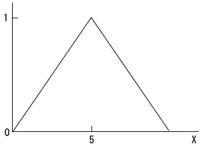
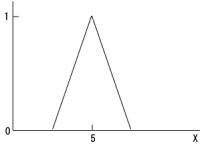
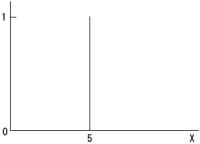
　前節でマムダニのファジィ推論を用いて推論結果を得る手法を示しました。しかし、実際の制御における入力とはファジィ集合ではなく数値です。入力がファジィ集合ではなく数値になるとはどういうことでしょうか？ここで、事実を与えるファジィ集合の曖昧さが少なくなった場合を考えます。曖昧さが少なくなるとは、メンバシップ関数で示される図の範囲が狭められるということです。そして、曖昧さが完全になくなるとは、メンバシップ関数で示される図の範囲がなくなりただ一つの値を示すことになります。入力が数値になるとは、「5ぐらい」というファジィ集合が「5」というクリスプ集合になる事を意味します。

→

→

　それでは、入力が数値である場合、演算過程はどの様に変形するのでしょうか？この場合、事実を与えるファジィ集合Aはクリスプ集合で表すことが出来るため、前件部を与えるファジィ集合A'との積集合は以下の図のようになります。



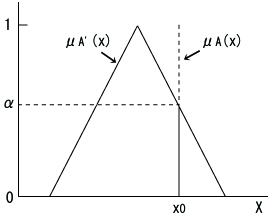
結局、これは事実を与える数値（仮にx0とする）におけるA'のメンバシップグレードをαにすることに過ぎません。つまり、αは次式で表されることになります。

α＝μA'（x0）

戻る 次へ