マムダニのファジィ推論（3）

　次に、前件部に二つの命題を有する場合を考えてみましょう。この場合、条件命題は以下のように規定されています。

条件命題：x1 is A1' and x2 is A2' , then y is B'.
事実　　　：x1 is A1 and x2 is A2.

結論　　　：y is B.　

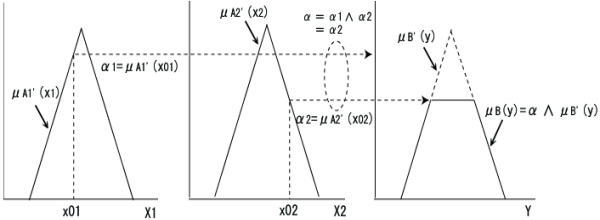
この時、A1とA2、A1'とA2'はand（「かつ」）による組み合わせです。これらはmin演算で結合されます。よって、結論ファジィ集合Bを得る演算は以下のように定めらます。





　上式を見て分かるようにμA1(x1)∧μA1'(x1)は前件部「x1 is A1」における入力A1の適合度（α1）であり、μA2(x2)∧μA2'(x2)は前件部「x2 is A2」における入力A2の適合度（α2）です。入力A1、A2をクリスプ集合で表される数値x01、x02であると仮定すると、αは次式で表されます。

α = α1∧α2 = μA1'(x01)∧μA2'(x02)

　前件部の命題が二つ以上になった場合も同じ手法でαを求め、推論結果を得ます。演算過程を以下に示します。



次へ 本文へ