ここではマムダニのファジィ推論について数式を追って詳しく説明をします。直接法では事実とファジィ関係から結論を導くために以下の演算を行いました。
B = A ○ R
それでは上式をメンバシップ関数で表すことを考えましょう。事実を与えるファジィ集合Aはメンバシップ関数μA(x)で与えられます。問題はファジィ関係Rですが、直接法によるファジィ推論では予めファジィ関係を定義しています。ファジィ関係は種々定義されており、その中で最も演算結果が良好であるといわれるのが、前件部と後件部をmin演算で結合するものです。マムダニのファジィ推論でもこれを採用しており、上式のファジィ関係Rは前件部のファジィ集合A'を与えるメンバシップ関数μA'(x)と後件部のファジィ集合B'を与えるメンバシップ関数μB'(y)とのmin演算で表すことができます。以上のことから、上式は以下のように書き換えられます。
この時、μB'(y)はmax演算におけるxに関して定数であるため、これを()の外側に出すことができます。従って、上式は以下のようになります。
()内の計算はAとA'の積集合を求め、そのメンバシップグレードの最大値を求めることです。それでは、求められたメンバシップグレードの最大値をαとおいてみましょう。αは前件部の適合度となります。
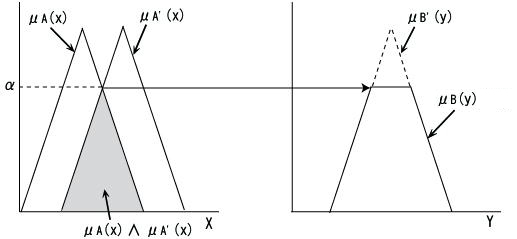
上式の意味はαとμB'(y)の値とを比較して小さい方を結果ファジィ集合Bのメンバシップグレードとすることです。こうして結果ファジィ集合Bが求められます。演算過程を下図に示します。
戻る 次へ