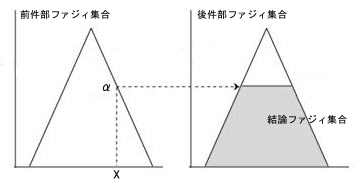
次に後件部のファジィ集合から結論を求める手法について説明します。ここで、事実として入力される数値をx、前件部の適合度をαとします。ここで、事実が前件部を充分満たすものであれば(αが1であるなら)、結論は後件部ファジィ集合そのものとなります。しかし、事実が前件部をある度合いでしか満たしていないのであれば(αが1でないのなら)、結論もそれに応じたものとしなければなりません。すなわち、後件部ファジィ集合を与えるメンバシップ関数(μ(B))に変化を加えた関数が結論となるわけです。
後件部より得られる結論は、前件部の適応度以上になることはありません。そのため、μ(B)をαでカットしたメンバシップ関数が結論となります。その概念図を下に示します。
また、条件命題が複数ある場合は、結論も複数となるため、それらを合成することで結果を得ました(ファジィ推論1を参照)。それぞれの結論はファジィ集合であり、それらはメンバシップ関数で与えられています。合成とはそれらメンバシップ関数で演算を行うことですが、和集合をとってやれば(「または」で結合してやれば)、それぞれの結論の特徴を損なうことのない結論を得ることができます。