先ほどの結果から、学習させたいパターン数が増えるほど 
を大きくとる必要があると考えられる。
そこで図 5.3 に加え、アルファベットの小文字のパターンを追加し、
52個のパターンを学習させる実験を行った。
図 5.9 を加え、 52個のパターンを学習させた結果を図 5.10に示す。
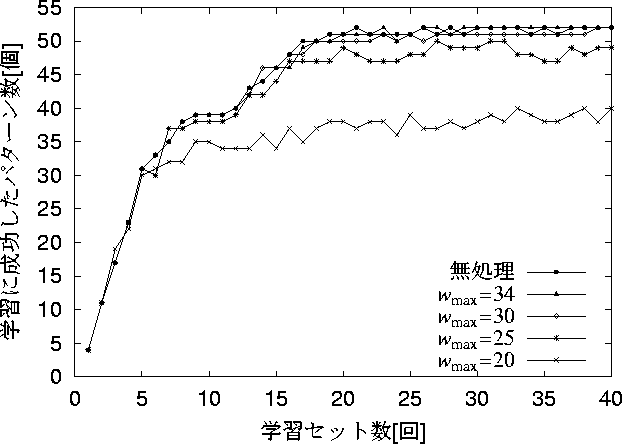
図 5.10: 学習パターン数52個での学習セット数と学習成功数の関係
図 5.3 の諸特性の意味は同様である。
パターン数を52に増やしても無処理の場合、
40セット終了時にはすべてのパターンを学習することができた。
また、 
、 
の時も学習に成功している。
しかし、 
、 
のときは、
すべてのパターンを学習することができなかった。
この値はパターン数26個の時では、全てのパターンを学習できる値である。
パターン数26個の時と同じく
規格化における標準最大値と学習できる個数との関連性を詳しく調べるため、
先と同じ条件で 
から 
まで 0.5 ずつ増やし、
40セット終了後の学習成功数を調べた。
この実験結果を図 5.11 に示す。
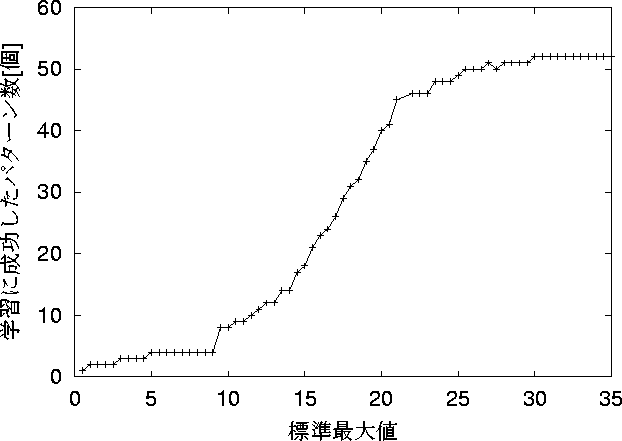
図 5.11: 学習パターン数56個での学習成功数の標準最大値特性
図 5.6で縦軸は40セット終了後の学習成功数、
横軸は標準最大値 の値である。
この結果より、標準最大値 が小さいほど、
多くのパターンを学習するのは難しくなり、
56個のパターンすべてを学習させるには、
を30程度にする必要があることがわかる。
