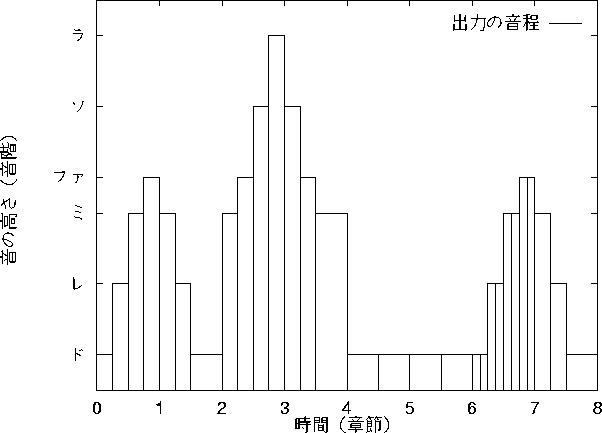
図 7.1: カオスニューラルネットの出力
入力層の素子数が10個で10万回学習した時の結果を表(7.1)に示す。
| ネット | 誤差 |
| カオスニューラルネット | 0.000154 |
| ニューラルネット | 0.000000 |
学習後のパラメータを読み込んで出力させた時の結果を図(7.1)に示す。 図中の縦軸は、音の高さを表していて、0.325がド, 0.025で半音ずれる。
この実験では、カオスニューラルネットより普通のニューラルネットのほうが良い
結果になった。
ニューラルネットにできてカオスニューラルネットできないはずはないので、
カオスニューラルネットの方は何かの原因で、誤差が減少するのが遅れたのでは
ないかと予想される。
しかし音符の高さが ![]() 、音符の長さが
、音符の長さが ![]() で間違いが生じるの対して、
で間違いが生じるの対して、
![]() とい値にはあまり意味がないと考えられる。
とい値にはあまり意味がないと考えられる。
次に入力層の素子数が2個で100万回学習した時の結果を表(7.2)に示す。
| 学習定数の変化 | 誤差 |
| 10万回毎に | 0.031792 |
| 10万回毎に | 0.026901 |
| 20万回毎に | 0.027100 |
| 20万回毎に | 0.212907 |
| 2倍の初期値で10万回毎に | 0.021093 |
| 2倍の初期値で20万回毎に | 0.022627 |
| 2倍の初期値で10万回毎に | 0.019099 |
一番良い結果が出た学習定数a,b,cが ![]() で10万回毎に変化させたときのパラメータ
を読み込み出力をした。その結果を図(7.2)に示す。
この図ではマイナス方向に教師信号があるが、これは見やすいようにしたもので、実際にはプラスである。上下対象になると学習できたといえる。
誤差が
で10万回毎に変化させたときのパラメータ
を読み込み出力をした。その結果を図(7.2)に示す。
この図ではマイナス方向に教師信号があるが、これは見やすいようにしたもので、実際にはプラスである。上下対象になると学習できたといえる。
誤差が ![]() という小さい値であるが、4音目からおかしくなった。
そこで、内部状態を学習後の値にして出力した。その時の結果を図(7.3)
に示す。これも4番目からおかしくなった。
この2つの出力結果は教師信号の全体的な特徴は持っているといえる。
しかし局所的には誤差は大きい。
という小さい値であるが、4音目からおかしくなった。
そこで、内部状態を学習後の値にして出力した。その時の結果を図(7.3)
に示す。これも4番目からおかしくなった。
この2つの出力結果は教師信号の全体的な特徴は持っているといえる。
しかし局所的には誤差は大きい。
![]() という値は平均なので、一時的に大きい誤差が出る可能性がある。
出力を入力に戻す時に規格化しているので、誤りが生じ、累積される
ので誤差が大きくなるのだと考えられる。
図を見るだけではよくわからないので再生して聞いてみると、あまり曲と呼べるような
ものではなかった。それは章節の区切りと音符の区切りがあってないからだと
考えられる。
という値は平均なので、一時的に大きい誤差が出る可能性がある。
出力を入力に戻す時に規格化しているので、誤りが生じ、累積される
ので誤差が大きくなるのだと考えられる。
図を見るだけではよくわからないので再生して聞いてみると、あまり曲と呼べるような
ものではなかった。それは章節の区切りと音符の区切りがあってないからだと
考えられる。