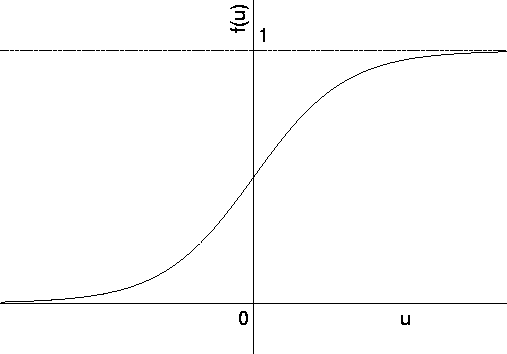
図 3.3: シグモイド関数
合原らのヤリイカの巨大軸索を用いた実験によりニューロン内にもカオス現象が存在することが明らかにされた[3]。 従来のニューロンのモデルでは、多数の入力の結合荷重としきい値作用をニューロンの特徴的な機能として採用し、モデル化を行なっていた。これは、忠実にニューロンをモデル化すると取り扱いを複雑にし、その本質を理解するのに障害になると考えられていたからである。 また、出力関数には全か無かの階段関数で表されている。
しかし、合原らの実験によると実際のニューロンは空間条件などを固定して注意深い実験を行なうと、その応答は、非周期的であり出力関数は急峻な立ち上がりを持つを持つことが分かった。 ニューロンの出力は図 3.3 のシグモイド関数のように連続的に応答が変わる出力関数になる。 よって、ニューロンの出力は全か無かの法則には従わないことになる。このことがニューロンのカオスを生じさせる原因となっている。 つまり、ニューロンのカオスは全か無かの法則の不成立ゆえに成立するのである。
そこで合原らにより、従来のニューロンに「カオス」の要素を取り入れたカオスニューロンが考案された。そのモデルは式(3.2) で表される。
ここで x(t+1) は時刻 t+1 におけるニューロンの出力、A(t) は時刻 t のおける外部入力の大きさ、 ![]() は不応性の項に対するスケーリングファクタ(
は不応性の項に対するスケーリングファクタ( ![]() )、k は不応性の定数
)、k は不応性の定数 ![]() 、g は軸索の伝達関数である。
不応性とはニューロンが興奮した後、一時的にしきい値が上昇する性質のことである。
また、膜電位や不応性は減衰されながらもしばらくの間残る。
関数 f はニューロンの内部状態と出力の関係を表し、通常はシグモイド関数を用いる。
その式は式(3.3) で表される。
、g は軸索の伝達関数である。
不応性とはニューロンが興奮した後、一時的にしきい値が上昇する性質のことである。
また、膜電位や不応性は減衰されながらもしばらくの間残る。
関数 f はニューロンの内部状態と出力の関係を表し、通常はシグモイド関数を用いる。
その式は式(3.3) で表される。
![]() は式(3.3) のシグモイド関数の立ち上がりの鋭さを表すパラメータである。
は式(3.3) のシグモイド関数の立ち上がりの鋭さを表すパラメータである。