5.1節での結果から、ノイズの数が10個の場合に26通り全てを想起
させることはできないのだろうかという疑問がでた。
人間の場合は、学習をより成功させるためにはたくさん学習すれば良い。
そう考えて、学習回数をこれまでの50回から、100回に増やして
実験してみた。この時、学習成功数の変化を詳しく知るために、 
の
測定幅を0.01きざみにする。
まず、学習回数が50回の時のグラフを図 5.6に示す。
次に、学習回数を100回にして実験を行なった。
この結果を図 5.7に示す。
図 5.6と図 5.7を比較する。
これらから、ノイズが0個の場合、 が7〜9までのときにおいて、
学習成功数が増えている。
学習成功数が増えることがわかったので、
ノイズを10個にして実験する。
まず、学習回数が50回の時のグラフを図 5.8に示す。
次に、学習回数を100回にしたグラフを図 5.9に示す。
ここで、 の測定の幅を0.1として測定した図 5.2
のノイズの数が10個である場合のグラフと
の測定の幅を0.01とした図 5.8とを比較してみると、
図 5.8において が1.6程度のときに学習成功数が26個に
なっている場合があることに気づく。
これは の測定幅を細かくとったので、全て学習できる点を
見つけることができたからである。
どちらにしてもノイズが10個であるときの学習成功数の
変化を表すグラフには違いないので、
ここでは、 の測定幅を0.01としたときの
学習成功数の変化について考えることにした。
図 5.8と図 5.9を比較する。
が1〜2までの間で学習成功数に変化が見られる。
予想と違い、学習を100回行なった方が学習成功数が減っている。
ノイズを10個いれたということは、
全体の約 
のドットが間違っているということになる。
学習回数を100回にすることで、
ノイズ入りの間違ったパターンを用いて何度も学習してしまうので、
想起して欲しいパターンを入力しても連想できなくなって
しまっていると考えられる。
以上により、ノイズが10個の場合には、0個の場合とは逆で
学習成功数は減ることがわかった。
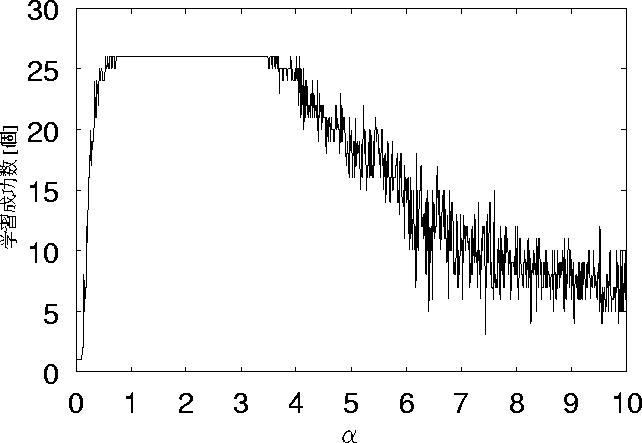
図 5.6: ノイズ0個、学習回数50回の時の学習成功数の変化
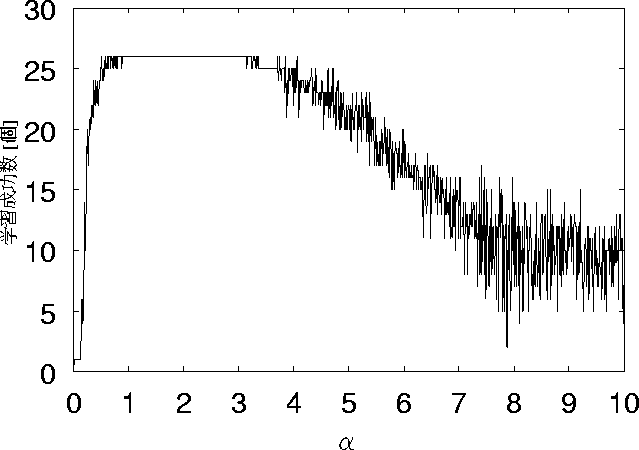
図 5.7: ノイズ0個、学習回数100回の時の学習成功数の変化
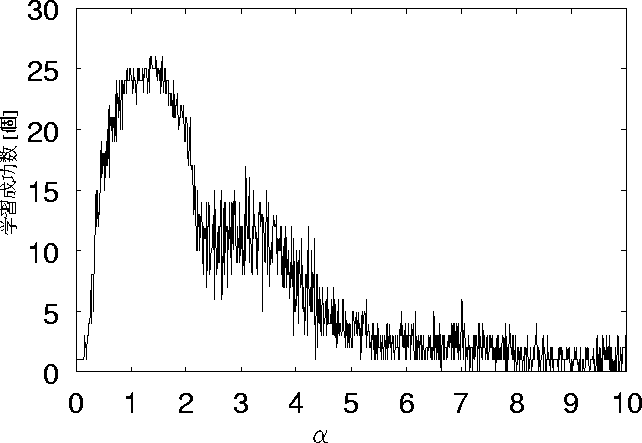
図 5.8: ノイズ10個、学習回数50回の時の学習成功数の変化
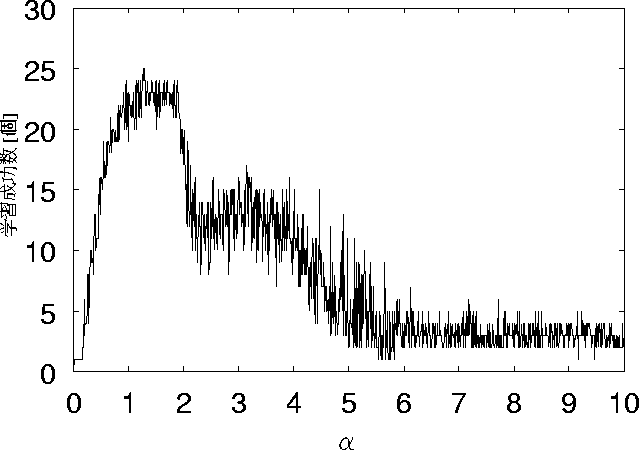
図 5.9: ノイズ10個、学習回数100回の時の学習成功数の変化