リセットというのは、それぞれのパターンを学習させた後、 次のパターンを入力する前に、 外部入力、相互結合の項、不応性の項を初期値の0に戻すということである。 この操作をすることにより、学習の効率があがるのである。 このとき結合荷重はリセットされない。 なぜリセットをすることで学習の効率が上がるのかというと、 2.5節で述べた、 「膜電位や不応性の情報は、減衰されながらも少しの期間だけのこる」 という特性の影響を受けなくなる、 すなわち、以前のパターンの影響を受けなくなるからである。
これまでの実験では、リセット無しの場合について行なってきた。 本節ではリセット有りの場合の学習成功数を測定し、 リセット無しの場合の学習成功数と比較することが目的である。
本実験では、リセット有り、無しについてノイズの数を0, 5, 10個
の場合について実験した。
ここでは、 
の値を0.01ずつ変化させて行なっている。
まず、ノイズが0個の場合について比較する。
リセット無しの場合を図 5.6、リセット有りの場合を
図 5.10に示す。
ここで、約0.6以下の点に注目すると、
リセット有りの場合、 がほぼ0であっても全てのパターンを想起できているが、
リセット無しの場合、想起があまりできていない。
また、リセット有りに対して、リセット無しは学習成功数の立ち下がりが
少し早く来ている。
これはリセットをすることにより、前の状態を引きずることが
ないために成功数が比較的多いのだと考えられる。
この結果により、ノイズ0の場合、リセットをした方が学習が
うまくいくことがわかった。
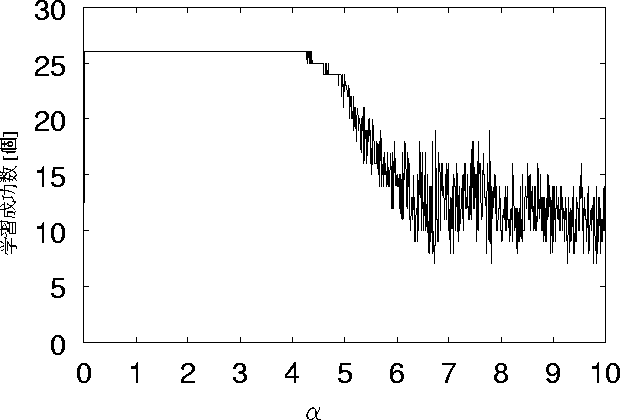
図 5.10: ノイズ0個、リセット有りの時の学習成功数の変化
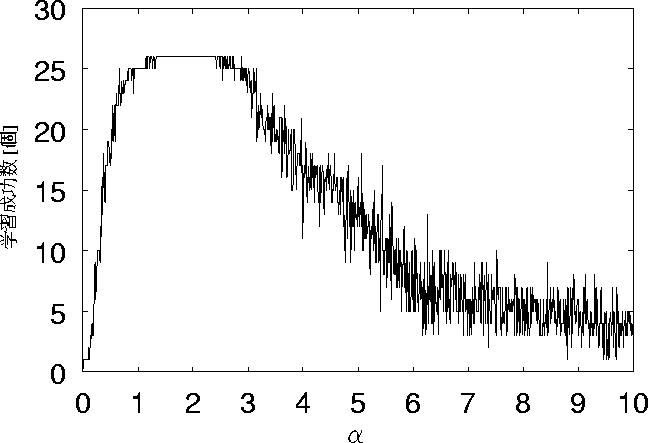
図 5.11: ノイズ5個、リセット無しの時の学習成功数の変化
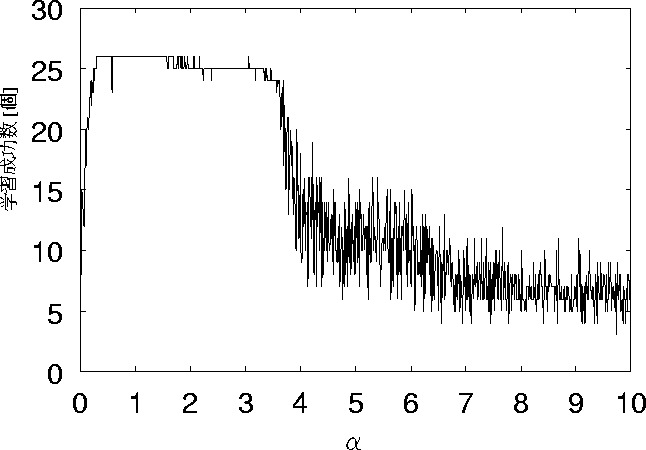
図 5.12: ノイズ5個、リセット有りの時の学習成功数の変化
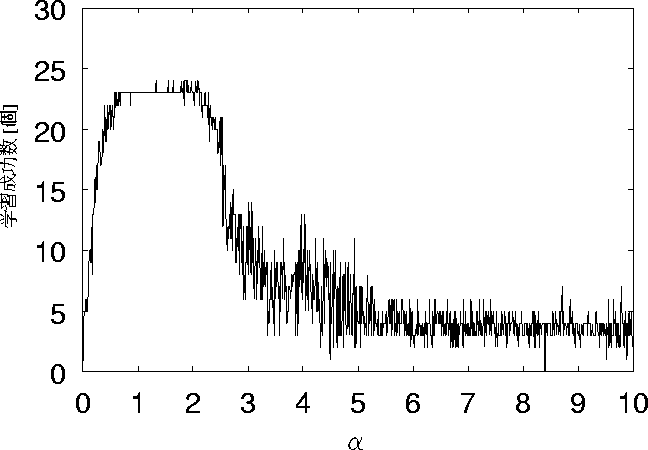
図 5.13: ノイズ10個 リセット有りの時の学習成功数の変化
次に、ノイズが5個の場合について比較する。 リセット無しの場合を図 5.11、リセット有りの場合を 図 5.12に示す。 この場合、立ちあがりの部分についてはリセット有りの方が早く 全てを想起できている。 しかし、1.9あたりから学習成功数がばらつき始めている。 ここでリセット無しをみてみると、1.5〜2.6ぐらいの値まで 学習が成功していることがわかる。 このノイズが5個の場合、リセット有り、無しの どちらが良いともいえなくなっている。
次に、ノイズ10個の場合について比較する。
リセット無しの場合を図 5.8、リセット有りの場合を
図 5.13に示す。
リセット無しの場合、 が1.5付近で26通り全て想起できている事がある。
しかし、リセット有りの場合には、26通り全て想起できることはなく、
しかも25個想起できることすらない。
全体的に両方のグラフの変化の仕方は良く似ている。
しかし、全体において学習成功数は明らかにリセット有りの方が少なくなっている。
ノイズが0であるとき、リセット有りの方がよく学習できていた。
しかし、ノイズが10になると、リセット無しの方がよく学習できるのである。
ノイズが10個入った場合、全てのドットの約 
にノイズが
入っていることになる。
このように、間違いが多いパターンを学習し、想起する場合には、
リセット無しで、前の状態に影響を受けた方が
学習がうまくいくことがわかった。
ゼロから学習するよりも、何らかの情報があった方が学習しやすいのである。