7.3.5 すべて変更したプログラム

 

  
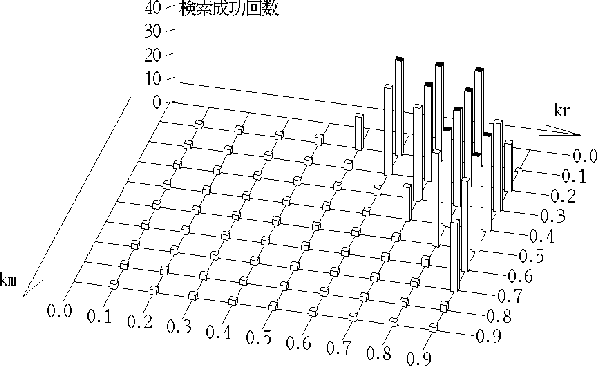
図 7.10: すべて変更したプログラムの検索結果

 

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

2 2 2 3 14 40 40 40 0

2 2 2 2 3 37 40 40 20

2 2 2 2 2 3 39 40 37

2 2 2 2 2 2 14 40 40

2 2 2 2 2 2 2 39 40

2 2 2 2 2 2 2 3 38

2 2 2 2 2 2 2 2 29

2 2 2 2 2 2 2 2 3

2 2 2 2 2 2 2 2 2

 

以上のすべて変更したプログラムの検索結果を図 7.10 に示す。 今度は40回すべて検索できるパラメータが9つある。 また、そのパラメータが固まっているため、 の間ならば、初期パターンをどのようにおいても、 どのパターンを検索しようとしても検索できるといえる。 検索回数が増え、数多く検索できるパラメータが表上で右上にずれているのは、 実験(3)と、実験(4)の傾向からであるといえる。 本研究の結果では、このシナプス前抑制関数に階段関数を用い、 特徴比較には距離を用い、 ネットワークにはカオスニューラルネットワークと 普通のニューラルネットワークを用いた結果が、 一番検索成功回数が多かった。 また、シナプス前抑制関数の階段関数のしきい値 gs を、 0.1から0.9まで9段階に変化させ、0.6以下なら良いという値を得た。 検索結果については付録 A に示す。