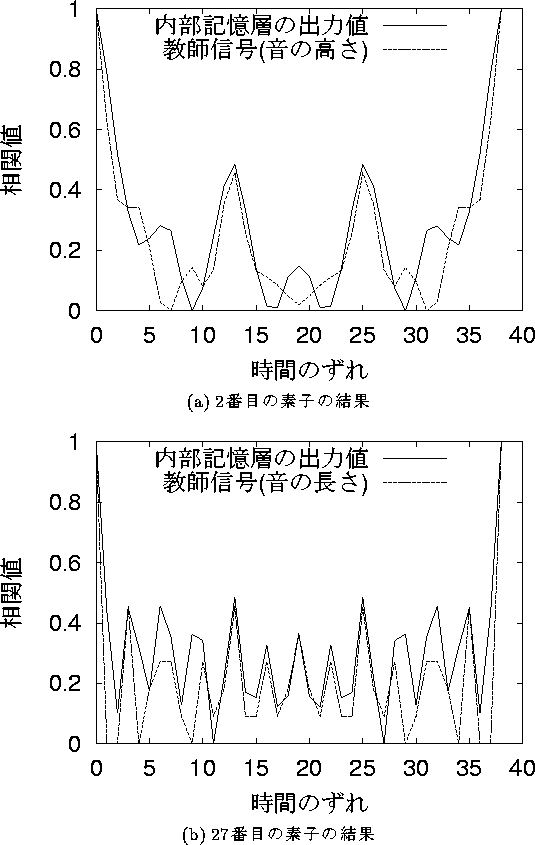
図 6.13: 自己相関の結果
初めに,個々の値ではなく相関関数を用いて時間的性質を調べた [10]. 内部記憶層の各素子の時間的変動について自己相関を求めた結果, その一例として中間層の素子数が30個,内部記憶層の素子数が35個の 場合について結果を示す. 内部記憶層中の2番目の素子のものが図 6.13 (a)のようになり, 別の素子での自己相関の結果は図 6.13 (b)のようになった. 但し,このグラフはその形状を見比べるために 縦軸の相関値は最大値が1.0, 最小値が0.0となるように値を変換したものであるため, 自己相関の計算結果そのものではない. この結果と教師信号のものと比べてみると, (a)は音の高さにおける相関値のグラフと非常に似ており, (b)は音の長さの相関値に似ている. 完全に一致していないのは, 別の教師信号の値も影響を及ぼしているものであると思われる. 実際にその出力値を時間的に並べたものが図 6.14 のようになる. 周期の開始点やその値が異なっているが, 時間的変動は教師信号と非常に似通ったものとなっていることがわかる. 以上の結果から内部記憶素子の時間的変動は 教師信号の値に影響してつくり出され, 教師信号の時間的変動を取り込んでいるといえる.