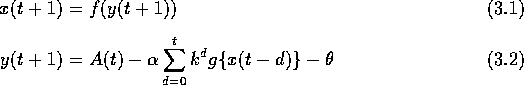
実際の神経細胞は容易にカオスを作成し、その応答は非周期的であるにも関わらず、 従来のニューロンモデルの応答はほとんど全て周期的である。 これは従来を考慮していなかった神経細胞がなんらかの特徴が、 カオスの生成に寄与していることを示している。
従来のニューロンモデルの出力は、全か無かの法則（階段関数）で与えられていたが、 合原らによれば、実際の神経細胞は空間条件など固定した注意深い実験を行なうと、 神経膜の活動電位生成過程は厳密には全か無かの法則には従わず、 図 3.1 シグモイド関数のように、 急激な立ち上がりだが、連続的に応答の大きさが変化する[2]。 このことがニューロンのカオス現象を生じさせている。 つまり、ニューロンにおけるカオスは全か無かの法則の不成立 によって成り立つ。
マッカロとピッツのニューロンモデルでは ニューロンの出力関数は階段関数で表されており、 その応答は周期的で、神経細胞モデルとしては不完全であると言える。 そこで合原らはカオスダイナミクスを有するカオスニューロンモデル を提案した。このモデルは式(3.2)で定義される[5]。
ここで x(t+1) は時刻 t+1 におけるニューロンの出力、
y(t+1) は時刻 t+1 におけるカオスニューロンの内部状態、
A(t) は時刻 t における外部からの入力の大きさ、
は不応性の影響の大きさを決定する係数( 
)、
は不応性の時間減衰項、 
は閾値である。
関数 f はニューロンの内部状態と出力の関係を表す式で、
通常は式(3.3)のシグモイド関数が用いられる。
