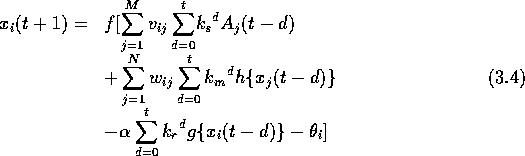


Next: 第4章 学習
Up: 第3章 カオスとカオスニューラルネットワーク
Previous: 3.2 カオスニューロンのモデル
カオスニューロンを相互結合で構成されたネットワークを
カオスニューラルネットと呼ぶ。
このカオスニューロンは、一般的にネットワーク内部からのフィードバック入力と
ネットワーク外部から受けるものとしてモデル化し、
任意のアーキテクチャに対応できるようにする。
M 個の入力と N のニューロン間の相互結合を持つ
カオスニューラルネットワークのi 番目ニューロンの
ダイナミックスは式式(3.4)で与えられる。
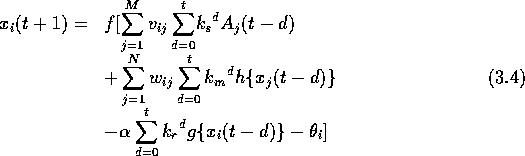
-
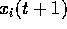 : 時刻 t+1 におけるi 番目のニューロンの出力
: 時刻 t+1 におけるi 番目のニューロンの出力 -
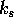 : 外部入力項に対する時間減衰定数
: 外部入力項に対する時間減衰定数 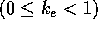
-
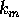 : 他のニューロンからのフィードバック入力項に対する時間減衰定数
: 他のニューロンからのフィードバック入力項に対する時間減衰定数
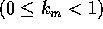
-
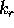 : i 番目ニューロン自身の不応性の時間減衰定数
: i 番目ニューロン自身の不応性の時間減衰定数 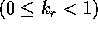
-
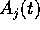 : j 番目の外部入力
: j 番目の外部入力 -
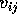 : j 番目の外部入力
: j 番目の外部入力 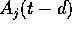 から i 番目
のニューロンへの結合係数
から i 番目
のニューロンへの結合係数 -
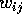 : j 番目のニューロンから i 番目のニューロンへの結合係数
: j 番目のニューロンから i 番目のニューロンへの結合係数 -
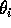 : i 番目ニューロンの閾値
: i 番目ニューロンの閾値
式(3.4)において、i 番目のニューロンの内部状態を、
項の持つ意味的に分離すると式(3.5)のようになる。
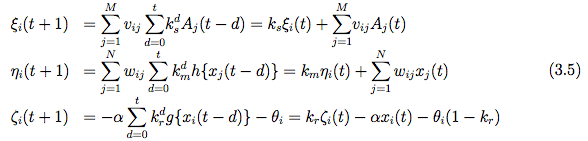
-
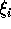 : i 番目ニューロンにおける外部からの入力に関する内部状態項
: i 番目ニューロンにおける外部からの入力に関する内部状態項 -
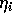 : i 番目ニューロンにおけるネットワーク内の他のニューロンから
のフィードバックに関する内部状態項(相互結合を表す項)
: i 番目ニューロンにおけるネットワーク内の他のニューロンから
のフィードバックに関する内部状態項(相互結合を表す項) -
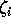 : i 番目ニューロンにおける不応性に関する内部状態項
: i 番目ニューロンにおける不応性に関する内部状態項
これを用いると、i 番目のニューロンの出力は、
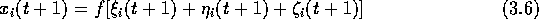
と表すことができる[5]。
式(3.5)と式(3.6)
を視覚的に表したものが図 3.2 である。
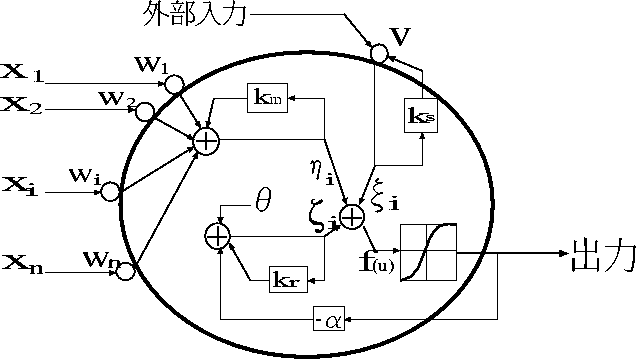
図 3.2: カオスニューロンモデル
Deguchi Toshinori
Wed May 15 13:53:18 JST 2002