入力パターンをアルファベットの大文字26個を順番にネットに入力して、
学習させ、想起することができた個数と 
のグラフを
図 5.2 に示す。
この場合 を0.005ずつ増やしていき、50回測定した場合である。
図 5.2には内部状態をリセットした場合と
リセットしない場合の2つを示す。
このネットワークは学習をする際に結合荷重を変化させ、 変化した回数が多ければ多いほど、学習できたことになる。 グラフを見ても分かるように結合荷重が0だと重みが 変わらないので、学習は全くしない。 結合荷重の値が大きすぎてもいけないことも分かる。 内部状態をリセットした状態だとリセットしていない場合より、 学習できていることがいえる。
今回入力として用いた学習パターンはアルファベットであるため、 白と黒の配列に特徴があり、学習しやすいパターンと、学習しにくいパターンがある。 良く似たパターンが存在するものほど学習しづらい傾向にある。
出力の例として入力パターンがMの場合を図 5.3 に示す。
これを見ても分かるように が0の時だと全てが黒の四角で学習は
全くしていない。0.005の場合はMに近い形だが想起できていない。
0.095の場合は入力パターンと同じなので想起できている。
0.245の場合はNのような形になっているので想起できていない。
これはNの影響が強かった出力と考えられる。
次に、結合荷重の変化量を表 5.2示す。 図 5.2より、学習成功数が26個ですべて想起できていて、 その周辺も全て学習が成功している結合荷重が0.05の場合で示す。 尚、この結合荷重の変化量は、20セットの変化量の総和である。
この結合荷重の変化量を見て分かるように相関学習とは違い、 結合荷重の変化量が大きいパターンと小さいパターンが存在した。 結合荷重の変化量が大きければ、より学習しているということなので Jが一番学習に時間がかかっており、逆にVが学習が一番早く終ったことがわかる。
また、表 5.2の場合は内部状態をリセットしていない場合なので、 リセットした場合と比較する。 リセットした場合の結合荷重の変化量を表 5.3示す。
| A = 2185 | B = 2341 | C = 2008 | D = 2178 |
| E = 2535 | F = 1905 | G = 1870 | H = 2366 |
| I = 2752 | J = 2618 | K = 2250 | L = 2125 |
| M = 2342 | N = 1691 | O = 2005 | P = 2069 |
| Q = 2128 | R = 2052 | S = 1613 | T = 2392 |
| U = 2526 | V = 1434 | W = 1561 | X = 1960 |
| Y = 2151 | Z = 2119 |
| A = 1516 | B = 1528 | C = 1552 | D = 1697 |
| E = 1941 | F = 1577 | G = 1091 | H = 1478 |
| I = 1553 | J = 1526 | K = 1525 | L = 1586 |
| M = 2299 | N = 1660 | O = 1420 | P = 1476 |
| Q = 1419 | R = 1201 | S = 1176 | T = 1611 |
| U = 1253 | V = 1180 | W = 1305 | X = 1057 |
| Y = 1562 | Z = 1201 |
リセットした場合としていない場合で比較すると、 リセットしていない方が結合荷重の変化量が多いのでより学習していることが言える。 これはリセットすると内部状態がその後の学習に以降に影響されず、リセットしないと 入力パターンが変化した直後はまだ前のパターンが影響され、しばらくの間、 前のパターンを出力しつづけるので、学習回数が多くなることが考えられる。
また、 が0.245の場合も比較する。
リセットありの場合を表 5.4、
リセットなしの場合を表 5.5に示す。
| A = 1208 | B = 1189 | C = 1167 | D = 1090 |
| E = 1280 | F = 885 | G = 1087 | H = 1264 |
| I = 1836 | J = 1655 | K = 1389 | L = 1020 |
| M = 1098 | N = 714 | O = 1045 | P = 1050 |
| Q = 1357 | R = 1132 | S = 1142 | T = 1500 |
| U = 1645 | V = 724 | W = 755 | X = 1451 |
| Y = 1182 | Z = 1381 |
| A = 695 | B = 458 | C = 523 | D = 667 |
| E = 585 | F = 495 | G = 334 | H = 458 |
| I = 464 | J = 407 | K = 577 | L = 578 |
| M = 766 | N = 549 | O = 514 | P = 420 |
| Q = 546 | R = 424 | S = 368 | T = 578 |
| U = 435 | V = 497 | W = 541 | X = 442 |
| Y = 527 | Z = 391 |
表 5.4と表 5.5を比較してみると、
= 0.05の時より、
明らかにリセットしない場合の方が学習した回数が多い。
これは図 5.2 からも分かるように、
リセットしている方は、
早い時点で学習が終るため、それ以降はほとんど学習されず、
総学習回数が減ってしまう。
逆にリセットしていない方は、新しいパターンの入力直後で過去に入力したパターンの
状態をひきずるため、
学習した回数が多くなる。
次に、学習回数を変化させた場合について検討する。
学習回数は25回、50回、75回、100回と変化させ、
を0.0005ずつ増やしていき1000回の測定を行なった。
また、それらの内部状態のリセットした場合、リセットしない場合で
比較、検討する。
10個のグラフを比べ、全体から言えることが、リセットした場合は学習成功数が多く、 25個ぐらいでほぼ一定の値が出る。 リセットしない場合は学習回数によって学習成功数の差が大きい。 リセットした場合とリセットしない場合でそれぞれ考察をする。
まず、リセットした場合について述べる。 図 5.4 、図 5.6 、図 5.8、 図 5.10、図 5.12 の5つを比較すると、 学習回数が多いとばらつきが少ないが 学習回数の少ないとばらつきがあることがわかる。
ここで、表 5.6 に学習成功数が26個から25個に
下がった時の の値をそれぞれ示す。
これを見て分かるように、学習回数が少ない方が26個 すべて想起できている範囲が長い。 また、26個学習している時の回数が多いのも学習回数が少ない25回の時が 一番多い。学習回数が25回の時は、実験結果より学習成功数が少なくなると 推測していたが、推測に反していた。
次に、リセットしていない場合について述べる。
図 5.5 、図 5.7 、図 5.9、
図 5.11、図 5.13
この5つを比較すると、リセットした場合に反して、学習回数によって学習成功数が
大きく変わっていることが分かる。
学習回数25回の時には、学習成功数が極めて少ないことがわかる。
学習回数が25回の場合以外は結合荷重の が0.1を越えた辺りから、
学習成功数が下がり始めるのが分かる。
しかし、25回の場合は0.04ぐらいから学習成功数が下がり始める。
学習回数25回と50回を測定した時点で、どれぐらいから
全体の学習成功数が多くなるか、検討するため学習回数40回の場合を測定した。
その結果学習回数40回では比較的学習成功数が多く50回と近いグラフになった。
しかし40回、50回、75回、100回になるにつれて、微妙ではあるが、
学習成功数が上がっている。
これらを検討してみると、内部状態をリセットしないので、
内部状態の変化がそれ以降の学習に反映され、
不応性等の時間減衰パラメータがそのまま残っているので
ネットワークは以前の入力をパターンを出力し続ける。
つまり、学習回数が少ないと想起しないまま
その以前の状態で新しいパターンを入力してしまうため、
学習回数が少ないと学習しにくくなる。
リセットしていない場合同様、 の値が大きすぎると
学習しにくくなることが、この図 5.5 、図 5.7 、
図 5.9、図 5.11、図 5.13からも
明らかである。
これらから、リセットした場合は結合荷重の値が大きすぎても、ある程度までは 想起できるが、 リセットしていない場合は結合荷重の値が大き過ぎると、想起しにくくなる。 よって結合荷重は適切な値をとると、想起しやすくなる。
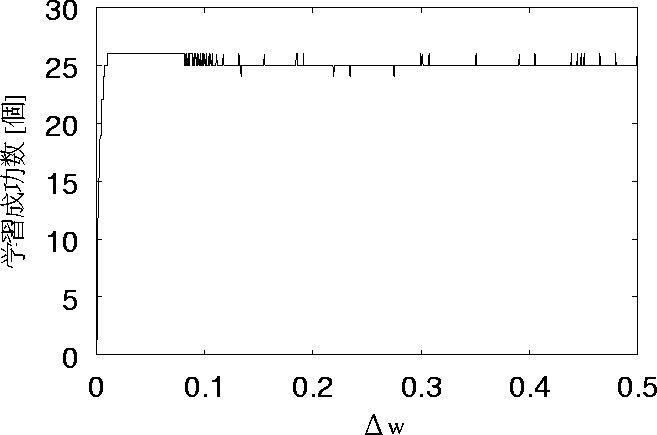
図 5.5: リセットして初期学習回数を50回とした場合の特性
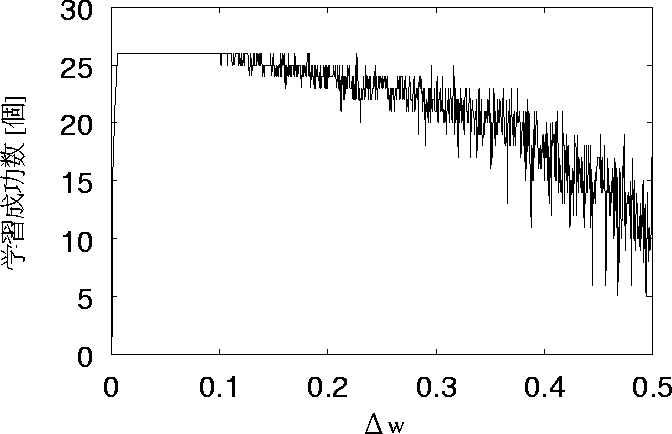
図 5.6: リセットせず初期学習回数を100回とした場合の特性
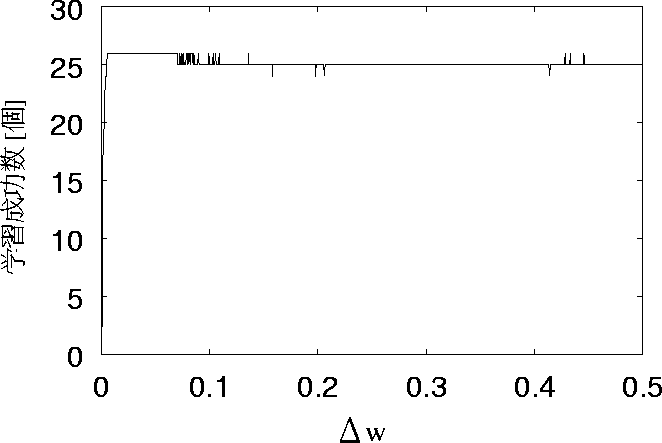
図 5.7: リセットして初期学習回数を100回とした場合の特性
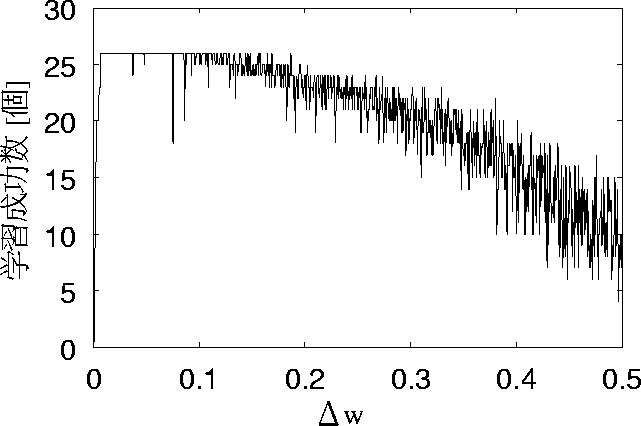
図 5.8: リセットせず初期学習回数を75回とした場合の特性
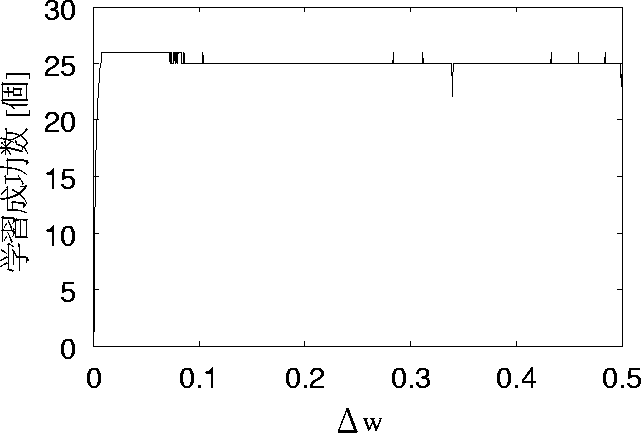
図 5.9: リセットして初期学習回数を75回とした場合の特性
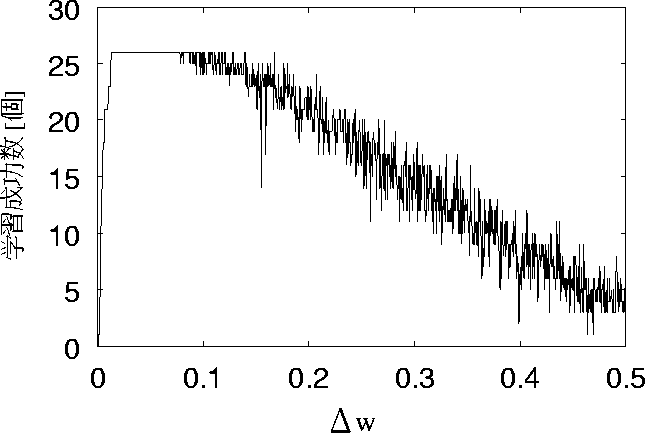
図 5.10: リセットせず初期学習回数を40回とした場合の特性
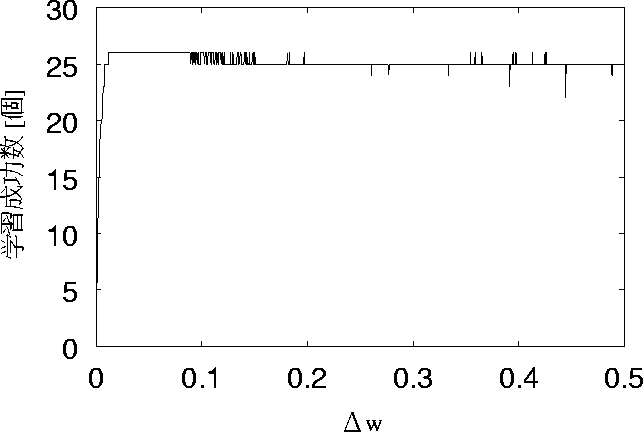
図 5.11: リセットして初期学習回数を40回とした場合の特性
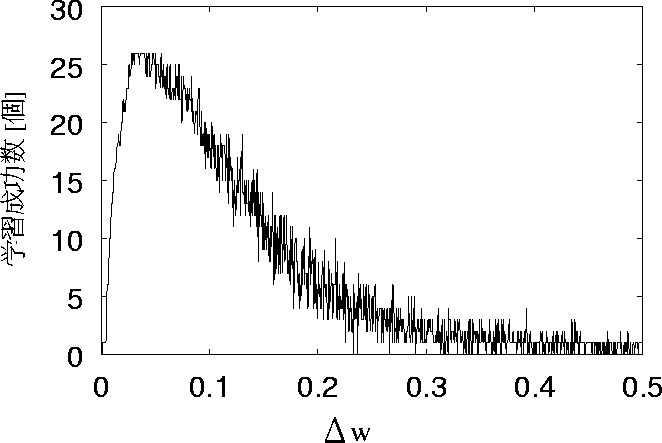
図 5.12: リセットせず初期学習回数を25回とした場合の特性
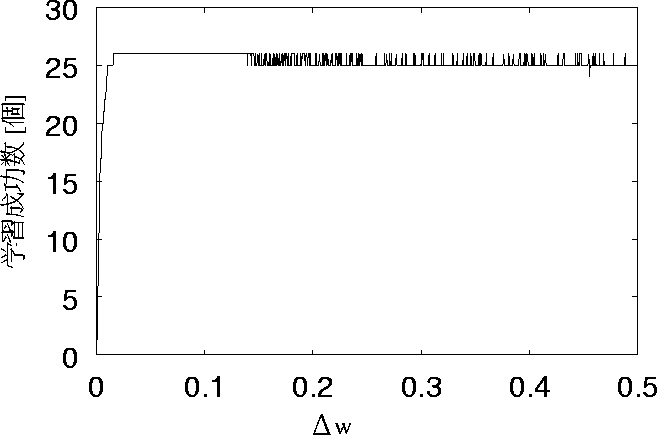
図 5.13: リセットして初期学習回数を25回とした場合の特性
リセットなしの結合荷重の変化量
リセットなしの結合荷重の変化量