逐次学習法において、未知パターンを記憶する際に、既知パターンを学習した
時にできた結合荷重値を利用していることを確かめるために、相関値の異なる
入力パターンを学習させ、記憶できるパターン数の違いを調べた。
また、 
が入力パターンsを完全に記憶しているかも調べた。
入力パターンは相関値が50%, 60%, 70%, 80%, 90%となるよう5種類作成した。
また、入力パターン数は1から100まで100通り実験した。
この中で、全てのパターンを記憶することができたものの内、入力パターン数が
最大のものを最大学習成功数とした。
この時、学習セット数は上限10000セットとし、10000セット未満でも全ての
入力パターンを記憶していたセットで学習を終了した。
については、入力パターンsを完全に記憶している
の割合( の記憶率)を調べた。
ここで、 の記憶率は、
で表される割合である。
学習成功数は表 5.2のようになった。 最大学習成功数は、相関値が高いほど多いことがわかる。 特に、相関値90%の入力パターンの場合では、素子数100に対し96パターンと、 素子数と同程度の数のパターンが記憶できている。 相関値が高い方が学習成功数が多いのは、相関値が高い方が、未知パターン学習時に 既知パターンの結合荷重値を多く利用することができ、その分1パターン記憶するのに かかる情報が少なくて済むためであると考えられる。
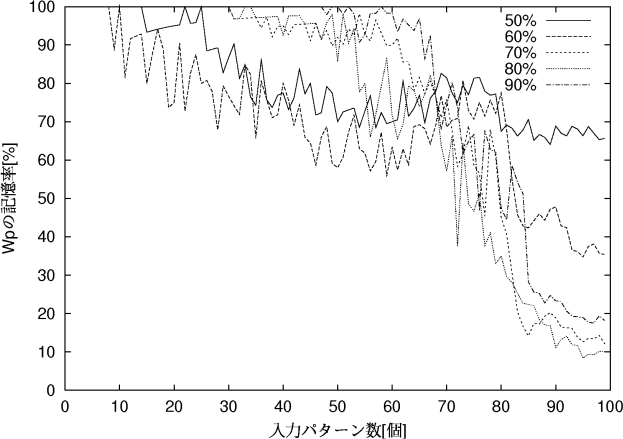
図 5.3: 各パターン入力中の結合荷重値変化分によるパターン記憶数
の記憶率は図 5.3のようになった。
横軸が入力したパターン数、縦軸は の記憶率である。
入力パターン数が少ないうちは、全ての が入力パターンを
記憶しているが、入力パターン数が増えてくると、入力パターンsを記憶していない
が増えてくる。
また、相関値50%, 60%では、少ない入力パターン数の内から の記憶率は
緩やかに下がっていく。
しかし、相関値70%, 80%, 90%では、いったん入力パターンを記憶していない
が出始めると、以後記憶率が急に下がり、やがて下がり止まる。
各 は、入力パターン間の相関の高い部分の情報の一部と、
入力パターンs特有の情報を記憶していると考えられる。
そこから、 の記憶率が下がり止まったということは、パターン間の
干渉のために、各 はこれ以上の情報を正しく記憶できなくなったという
ことであると考えられる。
そのため、これ以降記憶できるパターン数が増えなくなったと思われる。
このように、 の重ね合わせである 
が全ての入力パターンを
記憶しているのに、入力パターンを記憶していない が存在する
ということから、パターンを想起する時に、他のパターンの学習によって形成された
結合荷重値を利用していることが確かめられた。
学習に要したセット数は、入力パターン数80前後で大きく異なるため、 図 5.4に入力パターン数が80以下のときに全てのパターンを学習 するのに要したセット数、図 5.5に80以上のときのセット数と 分けて示す。 入力パターン数が80以下のときは、いずれの相関値の場合も緩やかにセット数が増加 しており、相関値が高い方が増加が早い。 入力パターン数が80以上のとき、相関値70%, 80%, 90%では学習に要するセット数が 非常に多くなる。 入力パターン数がネットワークが記憶できた最大パターン数に近付くと、どの相関値の 場合でも学習セット数の増加率が上がっているが、70%, 80%, 90%の場合は 特に著しく、70%では1500セット、80%では5500セット、90%の場合では 9000セット近くに達する場合がある。 入力パターンが正しく出力されるためには、うまく全てのパターンで干渉を 避けられるような結合荷重分布が形成されなければならない。 また、相関の高いパターンの学習によって作られる結合行列は似たものになると 考えられることから、入力パターン数が多く相関値も高い場合、パターン間の干渉を 避けるには、何度も結合荷重値を変化させ修正を繰り返さなければならないため、 学習セット数が増加すると思われる。
