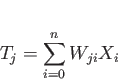 |
(4.2) |
である。
![]() は出力層のネット値で、中間層と同じようにして求めることができる。
図には書いていないが、出力層の
は出力層のネット値で、中間層と同じようにして求めることができる。
図には書いていないが、出力層の![]() 番目のニューロンの教師信号は
番目のニューロンの教師信号は![]() である。
である。
次に学習方法について説明する。ここで、学習するうえで必要な誤差![]() について定義する。
について定義する。
バックプロパゲーションの学習においては、子の誤差が小さくなるように結合荷重を修正していく。
まずは、中間層-出力層の結合荷重の学習を見ていく。結合荷重![]() に対する誤差の変化を見ればいいので、
に対する誤差の変化を見ればいいので、![]() を
を![]() で偏微分すればよい。これを式にすると、
で偏微分すればよい。これを式にすると、
となる。
![]() は学習係数と呼び、一度にどの程度結合荷重を変化させるかを示す。大きすぎると学習が大雑把になり、小さすぎると学習に膨大な回数がかかるようになるため調整が難しい。
は学習係数と呼び、一度にどの程度結合荷重を変化させるかを示す。大きすぎると学習が大雑把になり、小さすぎると学習に膨大な回数がかかるようになるため調整が難しい。
まずはそれぞれの微分の計算をする。
次に、出力をネット値で偏微分する。
最後に、ネット値を結合荷重で偏微分する。
これらの式から、修正量
![]() の式は以下のようになる。
の式は以下のようになる。
このようにして、出力層の結合荷重を求める。