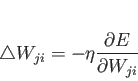 |
(4.5) |
結合荷重の修正量は、中間層-出力層と同じように、次の式で求められる。
出力層の結合荷重を計算するときは、![]() 番目の出力
番目の出力![]() のみに注目していたが、中間層の結合荷重を更新するときは
のみに注目していたが、中間層の結合荷重を更新するときは![]() 個の出力すべてが関係する。
この偏微分を行うには合成関数の微分を行う。これを行うと、中間層の結合荷重の修正量
個の出力すべてが関係する。
この偏微分を行うには合成関数の微分を行う。これを行うと、中間層の結合荷重の修正量
![]() を求める式は次のようになる。
を求める式は次のようになる。
それでは前節と同じようにこの式を計算していく。始めの2つは前節と同じなので省略する。
ネット値![]() を中間層の出力
を中間層の出力![]() で偏微分する。
で偏微分する。
中間層の出力![]() をネット値
をネット値![]() で偏微分する。
で偏微分する。
ネット値![]() を結合荷重
を結合荷重![]() で偏微分する。
で偏微分する。
これらの式より、結合荷重の修正量は次のようになる。
このようにして中間層の結合荷重の修正量を求める。[7]