前提条件

この実験では中間層の数を変化させてパーセプトロンに学習させ、中間層の数が学習過程における学習誤差の変化にどのような影響を及ぼすか調べる。 ただし棋譜は参考文献に示す、50万棋譜計画 - OWikiからのものを使用し、使用する約5万の棋譜の中に同一の棋譜は存在しないものとする。 その後、学習に使用した棋譜とは別の約5万個の棋譜をパーセプトロンに入力し、その時のそれぞれのパターンの誤差を見ることで考察していく。

なぜこのような手順を踏んでいるかというと、学習中の誤差を見るのではなく、学習後に改めて別の棋譜を使用して学習誤差を見ることによって、実践に非常に近い状況を作り出すことができるためである。

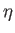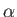各種学習定数は以下に示すとおりである。なお、ETAおよびALPHAは、式 5.2で出てきた学習係数$\eta$ と慣性項$\alpha$ のことである。

[各種係数]

入力層の数:128 (0〜63:白石の盤面パターン　64〜127:黒石の盤面パターン)

中間層の数:2, 4, 8, 12, 16

出力層の数:1

ETA=0.1

ALPHA=0.9