


Next: ベクトル空間法
Up: 実験に使用した技術
Previous: 主成分の選択方法
目次
潜在的意味解析
潜在的意味解析(LSA:latent Sematic Analysis)は、情報検索の分野において、
言葉の同犠牲や多義性に対処するために発展した統計的技法である。
すべての文書の背後には意味の構造が存在すると考え、これを行列の形に表現し、分解するところにLSAの特徴がある。行列として表現された語句と文書は、多変量解析の考えを適用し、数学的、統計的に分析対象とすることができる。LSAでは、さまざまな言葉で表現される意味の豊かすぎる部分を、行列の分解という形で取り除き、複数の語句の背後に共通して潜在する意味構造を抽出する。そのままの豊かさよりも、凝縮した構造のほうが、語句に留まらない意味の豊かさを効率的に表現できる可能性がある。 語句と文書を共起行列という形で表現し、潜在的な意味の構造を特異値分析で抽出するのがLSAである。このLSAの中身について説明する。
まず文書が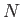 個のデータ行列
個のデータ行列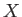 がある時、これを特異値分解すると左特異(ターム)ベクトル
がある時、これを特異値分解すると左特異(ターム)ベクトル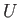 , 右特異(文書)ベクトル
, 右特異(文書)ベクトル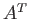 ,
, 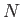 個の特異値を含むベクトル
個の特異値を含むベクトル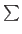 が得られる。
が得られる。
なお、ここでの各記号の意味は3.3項と同じであり、先に述べたように結合係数(固有ベクトル)が右特異ベクトルで与えられていることが分かる。データ行列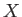 はこのように表せるので、式3.4の右辺の各行列から数行あるいは数列取り出すことで次元を圧縮することが出来る。その圧縮の方法としては、左特異ベクトルを用いて以下のように表せる。
はこのように表せるので、式3.4の右辺の各行列から数行あるいは数列取り出すことで次元を圧縮することが出来る。その圧縮の方法としては、左特異ベクトルを用いて以下のように表せる。
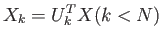 |
|
|
(3.13) |
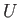 の成分は式3.9のように添字の若いものほど大きく、ここから最初の
の成分は式3.9のように添字の若いものほど大きく、ここから最初の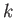 個を取り出して、
個を取り出して、 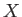 との行列積により元のデータ行列を
との行列積により元のデータ行列を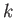 次元に縮約することが出来る。
次元に縮約することが出来る。
Deguchi Lab.
2013年2月28日
![]() 個のデータ行列
個のデータ行列![]() がある時、これを特異値分解すると左特異(ターム)ベクトル
がある時、これを特異値分解すると左特異(ターム)ベクトル![]() , 右特異(文書)ベクトル
, 右特異(文書)ベクトル![]() ,
, ![]() 個の特異値を含むベクトル
個の特異値を含むベクトル![]() が得られる。
が得られる。
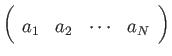

![]() はこのように表せるので、式3.4の右辺の各行列から数行あるいは数列取り出すことで次元を圧縮することが出来る。その圧縮の方法としては、左特異ベクトルを用いて以下のように表せる。
はこのように表せるので、式3.4の右辺の各行列から数行あるいは数列取り出すことで次元を圧縮することが出来る。その圧縮の方法としては、左特異ベクトルを用いて以下のように表せる。
![]() の成分は式3.9のように添字の若いものほど大きく、ここから最初の
の成分は式3.9のように添字の若いものほど大きく、ここから最初の![]() 個を取り出して、
個を取り出して、 ![]() との行列積により元のデータ行列を
との行列積により元のデータ行列を![]() 次元に縮約することが出来る。
次元に縮約することが出来る。