ベクトル空間法とは、文書を多次元空間上のベクトルとして表現し、 二つのベクトルを比較することにより類似度を調べるものである。 つまり、ベクトルの方向は文書の特徴であるので、二つのベクトルのなす角が小さいほど似ているということである。
![]() 個のタームを持つ文書
個のタームを持つ文書![]() を形態素解析し、各ターム毎の重要度を
を形態素解析し、各ターム毎の重要度を
![]() としたとき、 文書
としたとき、 文書![]() のベクトルは以下のように表される。
のベクトルは以下のように表される。
今、 ![]() 個のタームを持つ文書
個のタームを持つ文書![]() が文書
が文書![]() と どの程度類似しているのかということを考えたとき、 文書
と どの程度類似しているのかということを考えたとき、 文書![]() も式3.14から同様に
も式3.14から同様に
![]() となる。
これらベクトルDとベクトルEの類似度の計算は以下の式で実現できる。
となる。
これらベクトルDとベクトルEの類似度の計算は以下の式で実現できる。
ここで、 ![]() はベクトル
はベクトル
![]() とベクトル
とベクトル
![]() のなす角であり、
のなす角であり、
![]() は、文書
は、文書![]() と文書
と文書![]() の類似度である。
の類似度である。
以上のことを用いて、実際に計算を行う例を示す。例文としては以下のものを用いる。
| 例文D |
| ベクトルは大きさと向きを持っている。 |
| 基本ベクトルはある成分が1、それ以外は0のベクトルである。 |
| 例文E |
| ベクトルの成分による計算を行う。 |
次に、この例文![]() 、例文
、例文![]() を形態素解析し、重要度を計算したものを表3.1に示す。
を形態素解析し、重要度を計算したものを表3.1に示す。
| 用語 | 例文Dにおける重要度 | 例文Eにおける重要度 |
| ベクトル | 2.83 | 1.41 |
| 基本ベクトル | 1.41 | 0.00 |
| 成分 | 1.00 | 1.00 |
| 向き | 1.00 | 0.00 |
| 計算 | 0.00 | 1.00 |
この例文![]() 、例文
、例文![]() は式3.14の形式に表すと、
は式3.14の形式に表すと、
となる。重要度はそれぞれ、左の要素から( ベクトル , 基本ベクトル , 成分 , 向き , 計算 )と対応している。 次に、この2つのベクトルの大きさを計算する。
最後に式3.15より、この2つの例文の類似度を計算する。
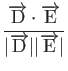 |
|||
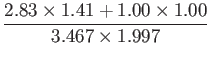 |
|||
よって、例文![]() 、例文
、例文![]() の類似度は0.72であることがわかる。
の類似度は0.72であることがわかる。