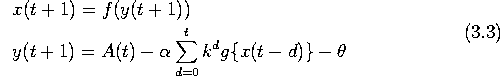
ニューロンの内部にもカオス現象が見られることが、 合原らのヤリイカの巨大軸索を用いた実験であきらかにされている [2]。 それによると、実際の神経細胞は空間条件などを固定した 注意深い実験を行なうと、その応答は非周期的であり 出力関数は厳密には階段関数ではなく、 急峻な立ち上がりを持った連続関数であることがわかる。 よってニューロンの出力は全か無の法則には従わない 連続的な値を持つことになる。 このことがニューロンのカオス現象を生じさせる原因となっているのである。 すなわち、ニューロンにおけるカオスは 全か無の法則の不成立によって成立するのである。
マッカロとピッツのニューロンモデルでは ニューロンの出力関数は階段関数で表されており、 その応答は周期的で、神経細胞モデルとしては不完全であると言える。 そこで合原らはカオスダイナミクスを有するカオスニューロンモデル を提案した。このモデルは式(3.3)で定義される。
ここで x(t+1) は時刻 t+1 におけるニューロンの出力、
y(t+1) は時刻 t+1 におけるカオスニューロンの内部状態、
A(t) は時刻 t における外部からの入力の大きさ、
は不応性の影響の大きさを決定する係数( 
)、
は不応性の時間減衰項、 
は閾値である。
関数 f はニューロンの内部状態と出力の関係を表す式で、
通常は式(3.4)のシグモイド関数が用いられる。
カオスニューロンを構成要素とするニューラルネットワーク をカオスニューラルネットワークと呼ぶ。このカオスニューロンの各々は、 一般にネットワーク内部からのフィードバック入力と ネットワーク外部からの入力を受けるものとしてモデル化される。
カオスニューラルネットワークの i 番目のニューロンの動的振舞いは 式(3.5)で表される。
は時刻 t+1 における i 番目のニューロンの出力、 
は
j 番目の外部入力 
から i 番目のニューロンへの結合係数、
は j 番目のニューロンから i 番目のニューロンへの結合係数、
はそれぞれ外部入力、ニューロン間の相互結合、
不応性の時間減衰定数である。
式(3.5)において、i 番目のニューロンの内部状態を、 項の持つ意味的に分離すると式(3.6)のようになる。
は外部からの入力を表す項、 
はニューロン間の相互結合を表す項、
はニューロン自身の不応性を表す項である。
これを用いると、i 番目のニューロンの出力は、
と表すことができる。 [4] 式(3.6)と式(3.7) を視覚的に表したものが図 3.5 である。
