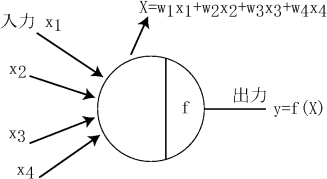
図 2.2: ユニット例(4入力1出力)
ユニットは、図 2.2に例示されているような多入力、1出力の素子が通常用いられている。
ニューラルネットワークにおいては、ユニットどうしが互いに神経繊維に対応する線で結ばれている。また、実際のニューロン間のシナプス結合と呼ばれる結合と同様に、信号は一方向にだけ伝わり、それぞれの結合部分に結合加重 ![]() をつけられて、結合されたユニットに出力される。
この結合加重が、ユニット同士の結合の度合いを表しているのである。
をつけられて、結合されたユニットに出力される。
この結合加重が、ユニット同士の結合の度合いを表しているのである。
このように重みがついたそれぞれの入力値 ![]() は、ユニットで総和 x がとられ、応答関数 f によって変換されて次のユニットへと出力される。
は、ユニットで総和 x がとられ、応答関数 f によって変換されて次のユニットへと出力される。
重みの値は、興奮性結合の場合は正の値、抑制性結合の場合は不の値を示す。また、この重みは学習をすることによって変化させることができる。
ユニットに入力された信号の総和 x は応答関数 f によって変換されるが、その応答関数はいくつかのものが考案されてきている。
図 2.3は、階段関数、あるいはヘビサイド関数と呼ばれるもので、この関数を用いればニューロンの出力を0か1で表すことが出来る。
図 2.4は、シグモイド関数と呼ばれる準線形の応答関数である。 第4章で説明するバックプロパゲーションという学習法において、微分可能な関数が必要となるため、そこで用いられる。