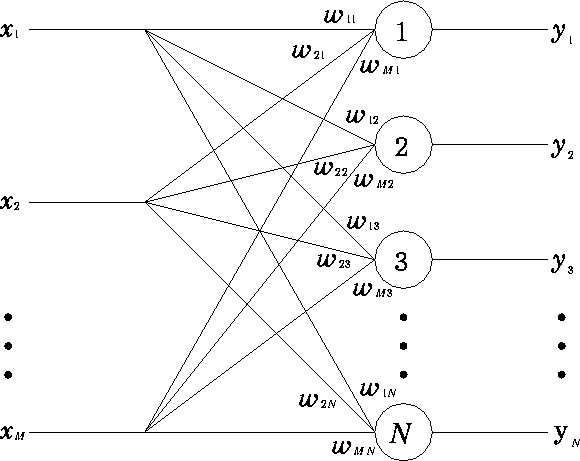
図 11: 連想記憶のニューラルネットの構造
連想記憶モデルは 1970 年代の始めに Nakano(1972),Kohonen(1972),Anderson(1972) の 3 者によって同時期に,しかも独立に提案された。 3 者のモデルにはそれぞれ特色があるが,ここでは,特定のモデルに偏らずに, 3 者のモデルに共通するような基本原理について説明する[10]。
ニューラルネットにおける連想記憶とは,一般に次のようなものである。 図 11 のように, N 個のニューロンに M 本の入力信号が加えられているニューラルネットを考える。
入力パターン ![]() (
( ![]() :入力信号 j がとる値)
と出力パターン(想起パターン)
:入力信号 j がとる値)
と出力パターン(想起パターン) ![]() (
( ![]() :ニューロン
i の出力信号がとる値)の組が複数個
:ニューロン
i の出力信号がとる値)の組が複数個 ![]() あって,
上記の P 個の入力パターンの内の 1 つをニューラルネットに入力した時に,
対応する出力パターン(つまり入力パターン
あって,
上記の P 個の入力パターンの内の 1 つをニューラルネットに入力した時に,
対応する出力パターン(つまり入力パターン ![]() に対しては
出力パターン
に対しては
出力パターン ![]() )を出力するように,
上記の入出力パターンを記憶することを連想記憶という。
また,連想記憶が学習する過程を記銘過程と呼び,神経回路網が入力パターンを
与えられることによって,何らかの出力をする過程を想起過程と呼ぶ。
)を出力するように,
上記の入出力パターンを記憶することを連想記憶という。
また,連想記憶が学習する過程を記銘過程と呼び,神経回路網が入力パターンを
与えられることによって,何らかの出力をする過程を想起過程と呼ぶ。
記銘する入力パターンと出力パターンとが一致\
![]() している連想記憶のことを
自己相関記憶,異なる連想記憶のことを相互相関記憶とよぶ。
自己相関記憶では,入力パターンと出力パターンとの組を複数個記憶するのでなく,
単純に復数個のパターンを記憶することになる。
している連想記憶のことを
自己相関記憶,異なる連想記憶のことを相互相関記憶とよぶ。
自己相関記憶では,入力パターンと出力パターンとの組を複数個記憶するのでなく,
単純に復数個のパターンを記憶することになる。
自己相関記憶は次のような意味をもつ。いくつかのパターンを記憶した後,
どのパターンとも正確には一致しないが,どれかのパターン ![]() と
最も近い入力
と
最も近い入力 ![]() をニューラルネットに与えるとする。
そのとき
をニューラルネットに与えるとする。
そのとき ![]() そのものを出力すれば,パターン
そのものを出力すれば,パターン ![]() から
パターン
から
パターン ![]() を「連想」したことになる。
このことを人間の脳の機能にあてはめると,例えば,
複数の文字の形を覚えている状態で,
形の崩れた文字を見せたときに,その文字がなんであるのか,
記憶しているものから最も近いものを答えることに相当する。
を「連想」したことになる。
このことを人間の脳の機能にあてはめると,例えば,
複数の文字の形を覚えている状態で,
形の崩れた文字を見せたときに,その文字がなんであるのか,
記憶しているものから最も近いものを答えることに相当する。
次に,ニューラルネットにおける連想記憶の特徴となる点を挙げる.
この点を解消することができる。
以上の特徴について,従来の方法と比較しながら説明する。(1) は,記憶する複数の入出力パターンの組の情報がそれぞれ, ニューラルネットのシナプス全体に分散され, 各々の情報が重なって記憶されることを意味する。 そのため,ニューラルネットが局所的に壊れても,従来の方法のように, 1 つの入出力パターンの組がまるごと記憶から失われることはない。
(2) は,(1) のようにシナプス全体に重なって 記憶されるために,記憶するパターンの組の数が増えても, 従来の方法で比較する回数が増えるように, 出力パターンを取り出すまでの動作は増えない。
(3) は,曖昧な入力パターンから正しい出力パターンを想起する能力の
ことである。
これは,ニューロンにしきい値作用を持たせた場合に持つ能力である。
自己相関記憶のところでも説明したように,
入力したパターン ![]() に近いパターン
に近いパターン ![]() が連想する
出力パターン
が連想する
出力パターン ![]() を想起する。
従来の方法では,近いパターンでも違うパターンとみなされるので,
出力が得られない。
を想起する。
従来の方法では,近いパターンでも違うパターンとみなされるので,
出力が得られない。