カオス的挙動とは，入力値が少しでも異なると， その振舞いが大きく変わることである. 例として，式(3.1)， 図 3.1 のような出力値がそのまま 次の入力値になるような系を考える.
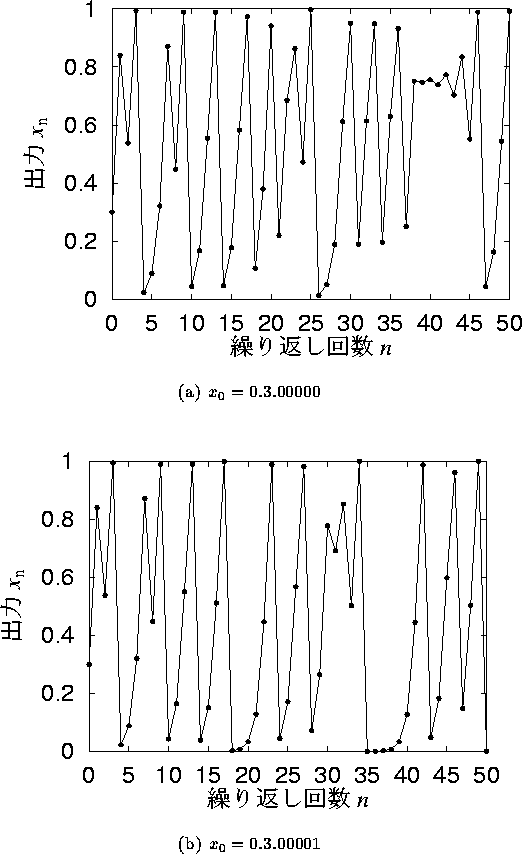
図 3.2: 初期値のわずかな違いで起こる系の挙動変化の様子
この式を用いて，実際に繰り返し計算をし，繰り返し回数 n と n 回目の出力
の関係を調べると，図 3.2 のように複雑な振舞いをしている.
この系はカオスであることが知られている.
また，この図の (a)，(b) ように初期値 
をそれぞれ 0.300000，
0.300001 と，わずか百万分の一だけ異なっている値を使って計算し比較すると，
n が 15 以下ではほとんど同じ挙動であるが，
n が15以上では全く違った挙動となっている.
このようにカオスでは，初期値のわずかな誤差でも，
系の状態変化に大きな影響を及ぼすことが示される.
このことからも, カオス状態においては, 実数のもつ無限の複雑さが次々に拡大されて, マクロレベルに現れる. カオスの完全な予測はディジタルコンピュータではその有限性のために, そしてアナログコンピュータではその不可解な雑音のために, 不可能なことが分かる[5].
