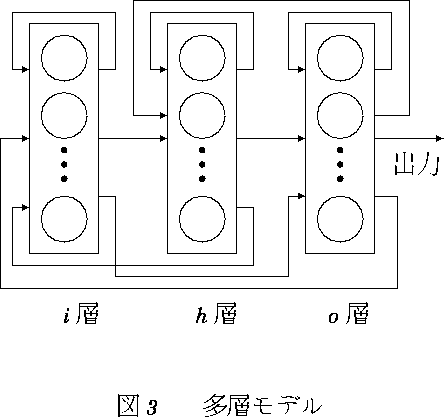
図 5.2: 3層モデル
前節までに述べたように、時系列の学習には前の状態を保持する層があればよいことになる。 同じパターンが1つ続けば2層、2つ続けば3層というように、再発部分系列が l 個続けば l+1 層あればよいことになる。
図5.2の3層モデルでは、現在の状態の1つ前の状態と2つ前の状態を記憶層が保持する。
例えば、図4.3で ![]() 、
、 ![]() とすると、
現在の状態が
とすると、
現在の状態が ![]() であったとしても、2つ前の状態が
であったとしても、2つ前の状態が ![]() なのか、
なのか、
![]() なのかが分かるため、次に想起する状態が
なのかが分かるため、次に想起する状態が ![]() であるということが分かる。
であるということが分かる。
この多層モデルの想起能力については、一昨年、本研究室の研究生であった山辺英孝氏によって確かめられた。
しかし、この多層モデルには、いくつかの問題点があげられる。
例えば、2層モデルではシナプス線束が4本必要であり、1層のニューロン数を n とすると、シナプス結合数は 4n となる。
この様に、全ての層の出力を入力としていては、図5.2のモデルではシナプス線束が9本、
l 層モデルでは ![]() 本のシナプス線束が必要となる。
これではハードウエアでの実現の際に、配線が非常に複雑になるという問題である。
また、電子計算機上でのシミュレートの際、計算量は
本のシナプス線束が必要となる。
これではハードウエアでの実現の際に、配線が非常に複雑になるという問題である。
また、電子計算機上でのシミュレートの際、計算量は ![]() となり、計算量がかなり多くなるため時間がかかるという問題もある。
これらの対策として、山辺氏はシナプス線束を減らすという方法で実験を行なった。
その結果、シナプス線束を減らしても想起能力には、たいして影響がないことが分かった。
となり、計算量がかなり多くなるため時間がかかるという問題もある。
これらの対策として、山辺氏はシナプス線束を減らすという方法で実験を行なった。
その結果、シナプス線束を減らしても想起能力には、たいして影響がないことが分かった。