不応性は相互結合を強めるために用いられ，不応性項の係数 
を変化させることは学習の効率を左右すると考えられる。そこで を変化させ，学習成功数を調べることにした。学習成功数とは，用意したパターンを学習させ，想起に成功したパターンの総数を表したものである。（今回の実験で最大学習成功数は26である） 図 5.3 は学習成功数特性で，横軸に不応性項の係数 を，縦軸にパターンの学習成功数をとっている。図ではそれぞれ2，4，20セットまでの学習における学習成功特性を示している。これはセット数が少ない時に学習成功数の変化が大きく，20セットを越えると，それ以降の学習成功数特性は大きく変わらないためである。
ここで が 0 の時は用意したパターンの学習が一つも成功しておらず， が 0 より大きい場合，学習に成功していることが分かる。また，ある程度不応性を大きくすることで，複数のパターンを学習することができることも分かった。
そこで，図 5.4 〜 図 5.6 は の測定範囲を広げ，個々のパターンの学習回数を25，50，100回と変えて学習させた結果である。 図 5.3 でも述べたが が0の時はパターンの学習が成功しておらず，これはパターンの学習回数に関係なく言えることである。これらから，不応性は学習を成功させるために必要なものだと言える。20セット学習をした場合， が 0 よりある程度大きい時は，全パターンの学習に成功しているが， が 5 より大きくなると，学習成功数は急激に減少していることが分かった。この時，ネットワークがどの様に学習をしているかを調べるため，結合荷重の変化回数を調べることにした。
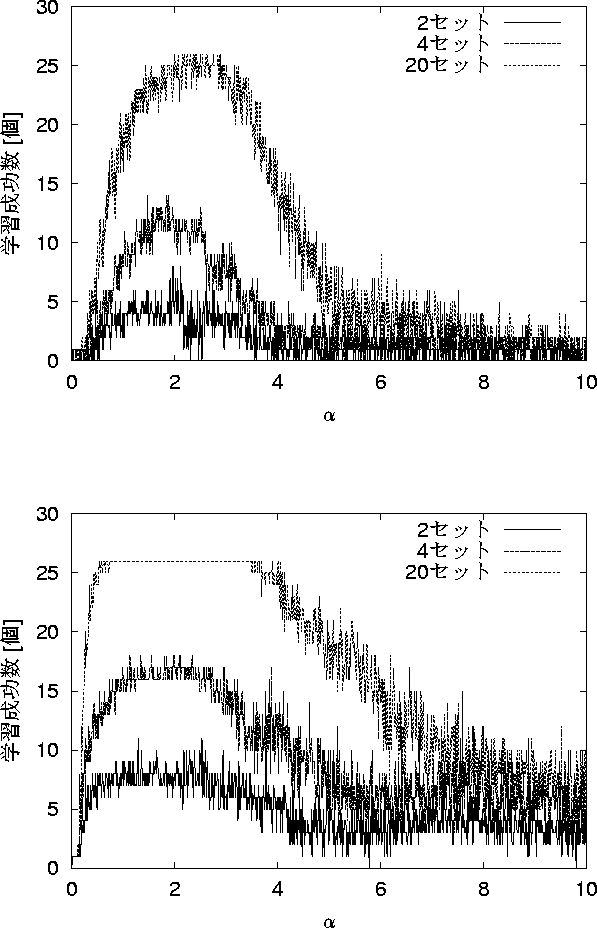
図 5.5: 学習回数50回の 学習成功数 - 依存性
図 5.4: 学習回数25回の 学習成功数 - 依存性
