ネットワークは結合荷重を変化することで学習をすることができ，変化する回数が多ければそれだけ学習をしようとしていると言える。パターンを学習できない場合の結合荷重の変化回数はどの様になっているのか，結合荷重の変化回数特性も同様に 
を変化させ，ニューロンがのべ何回結合荷重を変化させたか調べた。学習回数が50回のとき，20セット目の結合荷重の変化回数は図 5.7 〜 図 5.9の様になった。横軸を不応性項の係数αとして，縦軸にニューロンが変化した回数をとった。それぞれサンプルとして3個のニューロンを用意し，その変化回数を調べた。これらの図から，どの学習回数でも，ニューロンの変化回数は同じ形状をたどっていることが分かる。また図から が 5 を越えると，急激に結合荷重の変化回数が伸びていることが分かる。この場合， が 5 以下ならほとんど学習をすることはなく， が 5 以上の場合，20セット目であっても多くの学習をしていると考えられる。先の図 5.5と図 5.8 を照らしてみると，二つの特性は が同じ値を越えると急に変化していることが分かる。また，図 5.10 は学習回数が50回のネットワークの結合荷重総変化回数を表している。横軸にα，縦軸に総変化回数をとっている。結合荷重の総変化回数を2セットごとに調べた結果，何セットであっても，αが大きくなることで結合荷重の変化回数は増える傾向にあることが分かった。そしてαが大きくなり過ぎると，総変化回数は頭打ちになるまで増加していることが分かる。 が大きくなることで結合荷重の変化回数が増えているものの，パターンの学習は成功していない。これは，ネットワークがその都度学習しているパターンにより，それまで学習に成功したパターンを忘れ，再び未知パターンとして学習しているからだと考えられる。
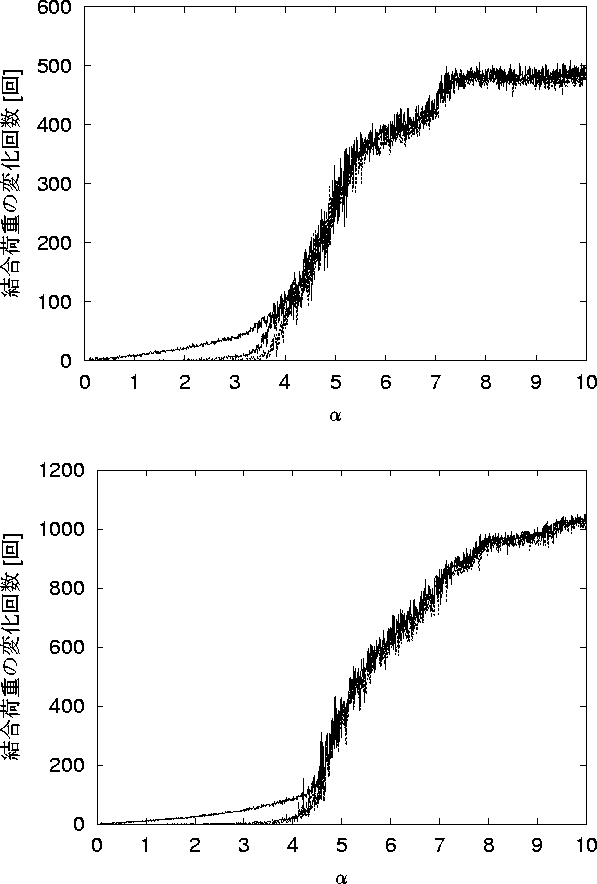
図 5.8: 学習回数50回の 結合荷重の変化回数 - 依存性
図 5.7: 学習回数25回の 結合荷重の変化回数 - 依存性
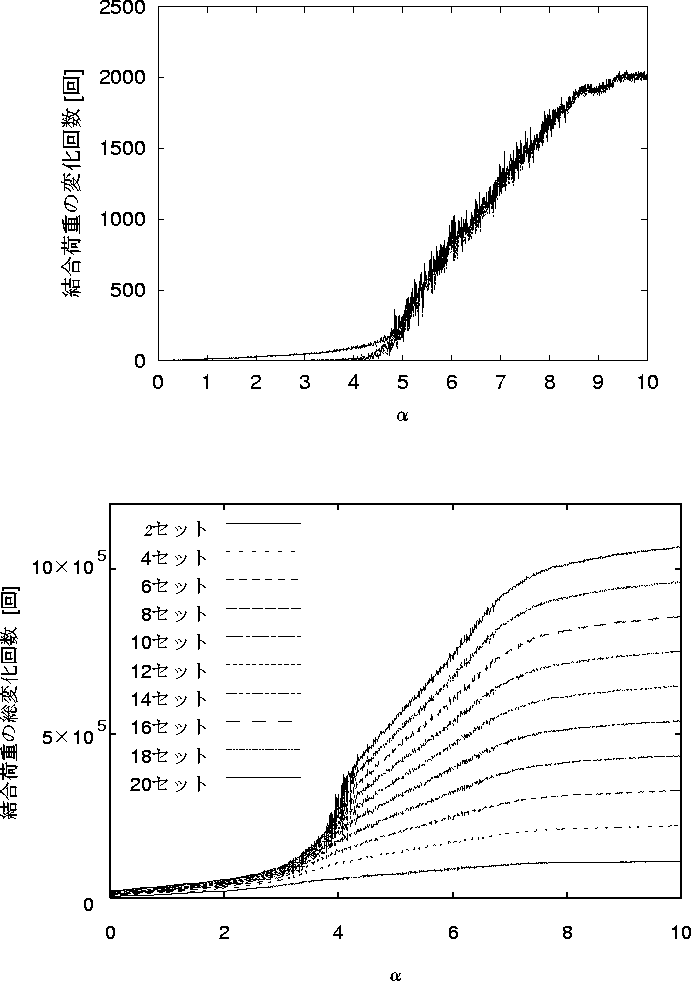
図 5.10: 学習回数50回の 結合荷重の総変化回数 - 依存性
図 5.9: 学習回数100回の 結合荷重の変化回数 - 依存性