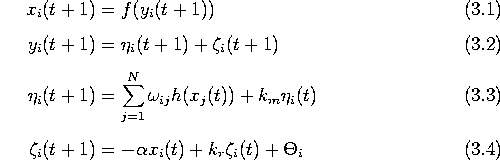
カオスニューロンのモデルを相互結合させ、 ネットワークを構成したものをカオスニューラルネットワークという。
カオスニューラルネットは次のような式で表される。
ここで、x(t+1)は時刻t+1でのニューロンの出力値、 f()は式(3.5)のようなシグモイド関数、
Nは入力の数、
はニューロンjからニューロンiへのシナプス結合の強さ、
h()はニューロンの軸索の変換特性を表す関数、
は入力に関する減衰定数 
、
は不応性に関する減衰定数 
、
はニューロンの出力と不応性の大きさの関係を与えるパラメータ、
はしきい値である。
式(3.2)の
第1項 
と第2項 
は、
次に説明する
カオスニューロンの2つの内部状態を表す。
式(3.3)は、
ニューロン間の相互結合を示し、
第1項は、
従来のニューロンと同様の他のニューロンからの入力信号の重みつきの総和である。
第2項は、
単位時間前の状態 
を減衰定数 倍して加算することによって、
過去の状態の影響を与えている。
式(3.4)は、
不応性の状態を示し、
第1項は、
単位時間前の出力 
を 
倍したもので、
ニューロンの出力が不応性に与える影響である。
第2項は、
相互結合と同様、
単位時間前の状態 
を減衰定数 倍して加算することによって、
過去の状態の影響を与えている。
また、
第3項は、
しきい値である。
これらの内部状態は、
式(3.2)で加算され、
式(3.5)のシグモイド関数を通して、
ニューロンiの出力 
となる。
不応性の項 が
ニューロン間の相互の力の項 より相対的に大きいとき、
カオスニューラルネットのカオスが激しくなり、
ネットワークは記憶したパターンを含む非周期的なパターンの系列を想起する。
時空間の加算の項が相対的に大きいときは、
静的な自己想起となる。
結合荷重の大きさを変化させると、 ニューロン間の相互の力の大きさが変わり、 これにより、 ネットワークの状態を制御することができる。
