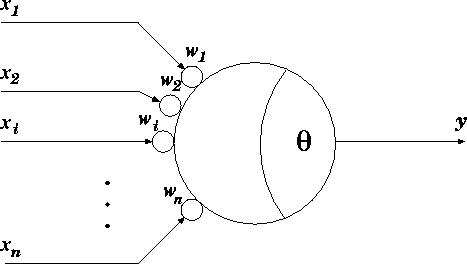
図 2.2: ニューロンのモデル
ニューロンは,樹状突起から多くの入力を受けとり, そして発火又は不発火という一つの信号を出力する。 また,他のニューロンの出力はシナプスを介して入力として与えられるが, この時,その入力がニューロンに及ぼす影響の強さは, 各ニューロン間によって異なると考えられる。 この影響の強さを「重み」と考えると, ニューロンは「重み付き多入力1出力素子」 であるといえよう。
ここで,一つのニューロンが n 個のニューロンから入力を受けているとする。
i 番目のニューロンの出力を ![]()
![]() ,それぞれの重みを
,それぞれの重みを ![]() とする。
単純に考えると,i 番目のニューロンからの影響は
とする。
単純に考えると,i 番目のニューロンからの影響は ![]() と表すことが出来る。
次に,簡単のため各ニューロンからの影響
と表すことが出来る。
次に,簡単のため各ニューロンからの影響 ![]() を単純に加算したものが,
ニューロンの入力総和になるものとする。
そして,この和が閾値θを越えた時,ニューロンが「発火」したと考える。
この「発火」そのものが,そのニューロンの出力となる。
このニューロンのモデル化したものを図3.2に示す。
を単純に加算したものが,
ニューロンの入力総和になるものとする。
そして,この和が閾値θを越えた時,ニューロンが「発火」したと考える。
この「発火」そのものが,そのニューロンの出力となる。
このニューロンのモデル化したものを図3.2に示す。
また,以上のことを式で表すと,
のようになる。
上式において,内部ポテンシャル u は重みつき入力総和 ![]() から閾値θを
引いたもので表されている。
そして内部ポテンシャル u0 を f(u) に代入したものが,
そのニューロンの出力となる。
f(u) は出力関数と呼ばれているもので,
一般に単調増加関数(右上がり)である。
入力
から閾値θを
引いたもので表されている。
そして内部ポテンシャル u0 を f(u) に代入したものが,
そのニューロンの出力となる。
f(u) は出力関数と呼ばれているもので,
一般に単調増加関数(右上がり)である。
入力 ![]() と出力 y のとり得る値としては,
2値のみを扱うモデルや,実数値を扱うモデルがある。
2値モデルの場合の出力関数は,
式(2.3)のように定義され,
図 3.2 のような階段関数と呼ばれるものを用いる。
と出力 y のとり得る値としては,
2値のみを扱うモデルや,実数値を扱うモデルがある。
2値モデルの場合の出力関数は,
式(2.3)のように定義され,
図 3.2 のような階段関数と呼ばれるものを用いる。
連続モデルの場合の出力関数は, 式(2.3)のように定義され, 図 3.2のように連続性のあるシグモイド関数と 呼ばれるものを用いる。