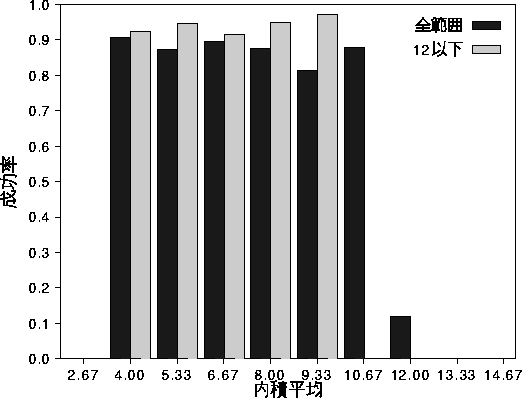
図 7.5: 相関内積と想起成功率の関係(直交なし,1 パターン 3 通り)
次に,もう一つの方法でこの結果をまとめる。 4 パターンを一つとしてではなく,1 パターンずつ別々に考え,このパターンに 関する 3 通りの内積値の平均をとる。これは, 図 7.5, 7.6 の「全範囲」ようになる。

図 7.5: 相関内積と想起成功率の関係(直交なし,1 パターン 3 通り)

図 7.6: 相関内積と想起時間の関係(直交なし,1 パターン 3 通り)
この成功率を見ると,内積平均 12 を境にして,それより小さいと成功率が高く, 大きいと全く成功していないことがわかる。 ここでさらに,4 パターン 6 通りの内積値がすべて 12 以下(ただし, すべて 12 ではない)であるパターンのみで同様に まとめると,図 7.5, 7.6 の「12 以下」の ようになる。この範囲では,さらに成功率が高く,想起時間もかなり短くなっている。
このように,この方法を用いれば,成功する条件をはっきりさせることができる。
そこで,今後の内積平均は,1 パターンごとの平均値を用いることにする。
また,「直交より少しずれたパターン」とは,使用した ![]() の
パターンの場合,図 7.5 から内積値がすべて 12 以下で,
全平均が 12 未満のものとなる。
詳しくは,直交について調べた上で,以上のような条件を加えて調べることにする
(第 7.3.3 節参照)。
の
パターンの場合,図 7.5 から内積値がすべて 12 以下で,
全平均が 12 未満のものとなる。
詳しくは,直交について調べた上で,以上のような条件を加えて調べることにする
(第 7.3.3 節参照)。
次節で,直交が含まれている場合はどのようになるかを調べる。