0.50 のパターンの検索
次に，要素平均が 
のパターンについて，
規則性が得られるかを調べた。
図 8.2 は，パターンの要素平均と想起時間平均の関係である。
この図にプロットしている値は，第 8.3 節で説明したように，
全検索が成功したもののうち想起時間平均が最小のものである。
また，この時の内部定数は，図 8.3, 8.4 に示している。
ただし，
これらの図で要素平均が 
のパターンについて，
何もプロットしていないのは，全く成功せずプロットするデータがないためで，
何も調べていないというわけではない。このことについての詳細は後述する。
まず，これらの図で気付くことは，0.37 付近で値が大きく変化していることである。
要素平均が 
の直交パターンは規則的に作成できるが，0.38 以上の
パターンは，各要素ごとの 0, 1 の配置の仕方が複雑になるため，
これが影響しているものと考えられる。 
付近についても，
不規則的な変化があるが，同様な原因が考えられる。
次に，全く成功しなかった要素平均 のパターンについて検討する。
まず，その原因を調べるため，ニューロンの出力パターンの変化を調べた。
その結果，短時間で目的のパターンが出力されるが，
周期的に雑音が入ったパターンも出力され，収束しないことがわかった。
これは，0.25 のパターンに近いので各学習パターン間のポテンシャルが低く，
各パターン間は素早く移動できる反面，収束点の溝が浅くなっているので，
収束しないものと考えられる。
また，要素平均が 0.25 のパターンは各要素ごとの平均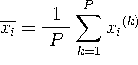 
もすべて 0.25 と
なるが， のパターンは一部分だけ 0.00, 0.50 となり，
その部分が雑音となるものと考えられる。
0.30 以上のパターンは，この各要素ごとの平均が 0.00, 0.50 となる要素が，
のパターンに比べ増加するため，その影響が小さくなると考えられる。
最後に，各パラメータについて検討する。
， 
については，それぞれ 0.4，0.6 付近になっていて，
規則性があるようにも考えられる。
前節でも検討したが，
要素平均が 0.75 のパターンの場合はこの値から大きくはずれているので，
反転パターンである要素平均が 0.25 のパターンで検索する場合での
最も検索に適したニューロンの状態に，
なるべく近づけた結果ではないかと考えることができる。
は，前述したようなパターンの作成方法の影響によるためか，
要素平均が 
の場合を除けば，
全体的に要素平均が大きいほど値を小さくした方が短時間で検索できることがわかる。
