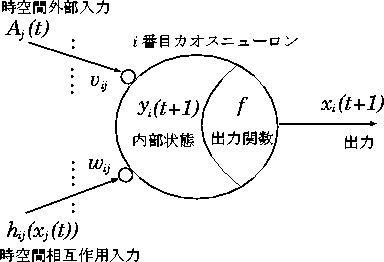
図 3.1: カオスニューロンモデル
実際のニューロンは、容易にカオスを生成するにもかかわらず、 2.2節で述べたような従来のニューロンモデルは、 ほとんどが周期的である。 このことは、従来のモデルでは考慮していなかった実際のニューロンの 何らかの特性が、カオスの生成に寄与していることを示している。
従来のモデルでは、「ニューロンの活動電位の生成過程は全か無の法則に従う 階段関数で与えられる」と考えられていた。 しかし、これはあくまでも伝搬性活動電位に関するものであり 空間固定の条件で注意深い実験を行なうと、実際の神経膜の活動電位生成過程は、 厳密には全か無の法則には従わず図 2.3 のシグモイド関数の ような連続的に大きさが変化する活動電位特性を有する。 そしてこのことがニューロンのカオスを生み出している。 つまり、ニューロンのカオスは全か無の法則の不成立ゆえに 成立するのである[6]。
カオスニューロンの相互結合で構成されたネットワークを カオスニューラルネットワークと呼ぶ。 一般にニューロンのモデルを考えるにあたっては、
このような観点から、単純な法則がカオスを含む複雑な応答特性を生み出す カオスニューロンモデルで構成されたカオスニューラルネットワークを考える。 カオスニューラルネットを構成する i 番目のニューロンの入出力の様子を、 図 3.1 に示す。ここで各ニューロンは、
ここで
![]()
M:外部からの入力総数
![]()
![]()
![]()
![]()
N:ニューラルネットワークを構成するカオスニューロンの総数
![]()
![]()
![]()
![]()
式(3.1) のカオスニューロンモデルは、 実際の生物のニューロンが有する軸索小丘部のアナログ的出力関数、 多数の外部入力やフィードバック入力の時空間的荷重および 神経膜の不応性をモデル化したものである。
式(3.1) の i 番目のカオスニューロンモデルの
ダイナミクスは、それと等価で数値計算が容易な以下のような3つの内部状態変数
![]() のダイナミクスに書き換えることができる。
のダイナミクスに書き換えることができる。
![]()
![]()
![]()
ここで、式(3.2),(3.3),(3.4) はおのおの 式(3.1)右辺の関数 f の( )内の第1項,第2項, および第3,4項に対応する i 番目のカオスニューロンの内部状態変数で、 以下のようになる。
上式(3.5) 〜式(3.7) で定義した 各項の和をニューロンの内部状態 とすると、i 番目のニューロンの出力は式(3.8) で表される[4]。
ここで、関数 f は式(2.4) で表されるようなシグモイド関数とする。
また式(2.4),(3.2),(3.3),(3.4) を視覚的に表すと図 3.2 のようになる。