


: 安定性と可観測性
: sysconh16
: リアプノフの安定性理論
対象とするシステムを線形システムに限った場合には,リアプノフの安定性理論から次の結果が得られる.
定理5.6(線形システムに対するリアプノフの安定定理)システム(5.1):
の原点が漸近安定であるための必要十分条件は,にんいに与えられた正定行列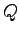 (
(
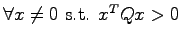 )に対して
)に対して
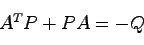 |
(18.1) |
となるような正定行列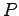 がただ1つ存在することである.
がただ1つ存在することである.
証明 十分性を示す.(18.1)を満たす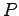 が唯一存在すると仮定する.
このとき
が唯一存在すると仮定する.
このとき
ととれば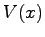 は正定で,かつ
は正定で,かつ
であるから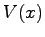 はリアプノフ関数であり,明らかに
はリアプノフ関数であり,明らかに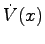 は負定関数であるから定理5.5より原点は漸近安定である.
は負定関数であるから定理5.5より原点は漸近安定である.
必要性を示す.システムの漸近安定性より入力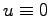 におけるシステムの解
におけるシステムの解
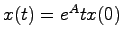 は時間と共に
は時間と共に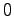 に収束する.したがって,任意に与えられた正定行列
に収束する.したがって,任意に与えられた正定行列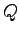 に対して
に対して
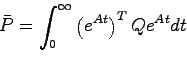 |
(18.2) |
により有限な正定行列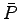 が定義できる.また
が定義できる.また
であるから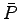 が(18.1)式の1つの解である.さらに(18.1)式を満足する任意の解
が(18.1)式の1つの解である.さらに(18.1)式を満足する任意の解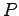 に対して,(18.2)式より
に対して,(18.2)式より
となるので,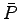 が(18.1)式のただ1つの解であることが示された.
が(18.1)式のただ1つの解であることが示された.
この定理において重要な点は,線形システムについては,リアプノフ関数を(18.1)式により求めることができるということである.
例5.7 システム
の安定性をリアプノフの安定条件を用いて判別する.正定行列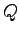 として
として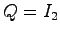 を取り
を取り
とおくと,(18.1)式より
が得られ,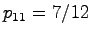 ,
,
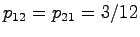 ,
,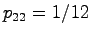 となる.これより
となる.これより
となる.さらに任意の
![$x = [ x_1\; x_2]^T$](img883.png) に対し
に対し
より,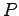 は正定行列である.よってシステムは漸近安定である.
は正定行列である.よってシステムは漸近安定である.
endo
平成16年6月30日
![]() が唯一存在すると仮定する.
このとき
が唯一存在すると仮定する.
このとき
![]() におけるシステムの解
におけるシステムの解
![]() は時間と共に
は時間と共に![]() に収束する.したがって,任意に与えられた正定行列
に収束する.したがって,任意に与えられた正定行列![]() に対して
に対して
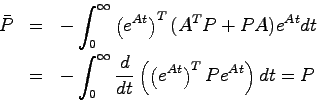
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}
-1 & 0 1 & -2 \end{array}\right] x + \left[ \begin{array}{c}1 0\end{array}\right]u
\end{displaymath}](img875.png)
![\begin{displaymath}
P = \left[\begin{array}{cc}p_{11} & p_{12} p_{21} & p_{22} \end{array}\right]\end{displaymath}](img877.png)
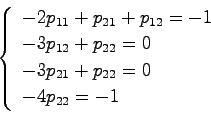
![\begin{displaymath}
P=\frac{1}{12}\left[ \begin{array}{cc}
7 & 1 1 & 3
\end{array}\right]
\end{displaymath}](img882.png)