この節では、 実際に学習させた結果より考察を行なう。 今回のエノン写像の学習には、 エノン写像が簡単なダイナミクスで表されるため、 中間層の中のニューロンの数は比較的少ない30個とした。
では、
実験結果について考察する。
まず、
学習回数 n を 1000000 回一定にして、
安定化定数 
を変化させていき、
学習に最適な を決定する。
学習定数 
は本実験を通して 0.05 とする。
図5.2にその結果を示す。
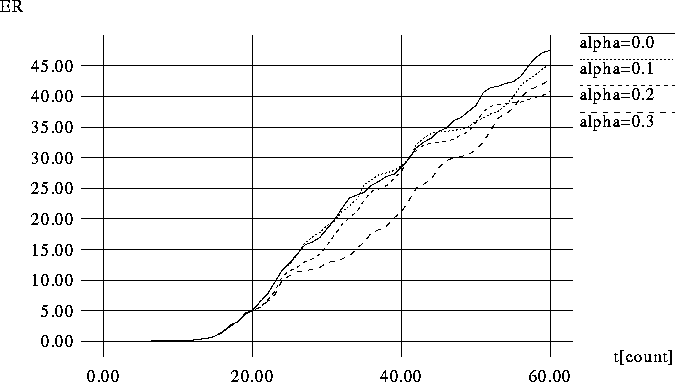
図 5.2: を変化させた時のER（学習回数 1000000 回)
図を見ると、 t=14辺りでどの線も立ち上がっている。 線が急に立ち上がるのは、 誤差が少しずつ蓄積され、 一度道を外れると似たような点を通るだけで、 二度と同じ点を通ることがないので、 誤差が蓄積されてどんどん距離が離れていくからである。
グラフの立ち上がり、
即ちどの点まで正確に学習できているかということについては、
に余り依存せず t=14〜15 ぐらいであるが、
その後徐々に誤差が増加してゆき、
教師信号から遠ざかっていく。
そして t=60 の段階では 
のグラフが最も ER が小さく傾きも小さくなっている。
この結果より、
学習回数を変化させて行なう実験は として行なう。
次に、
先ほどの実験結果によって決定した を使用して、
学習回数を増すことによってどれだけダイナミクスを正確に学習することができるかを実験する。
実験は、
学習回数 n を 10000、50000、100000、500000、1000000、
5000000、10000000と７通りに変化させて行なったが、
ここでは、
その中でも顕著に違いを確認することができた n= 10000、100000、1000000、5000000、10000000の５通りの実験結果を示し、
それを比較しながら学習効果について考察する。
図5.3〜図5.7に実験結果を示す。 図の左側に学習直後の教師信号を初期値として与えたネットワークのダイナミクスを示す。 右側には、 その初期値をエノン写像の式を代入した時の式のダイナミクスを示す。 これはつまり、 教師信号の続きということになる。
左右の図を見比べると、 n=10000 の図5.3では、 ほとんど学習が行なわれておらず、 その外形を多少残しているだけであることがわかる。 これはやはり、 学習回数があまりにも少なく学習が途中で打ち切られてしまったためと考えられる。 しかし、 n=100000 の図5.4のようにある程度学習回数が増えると、 外形はほとんど右側の図と一致する。 これは、 式のダイナミクスをほぼ学習しているということを裏付ける結果であるといえる。 しかし、 よく観察すると図の尖った部分や、 線と線の間の間隔などは微妙に異なり、 それも学習回数を増すことにより近付いてはいるものの、 完璧に一致しているとはいえない。
式のダイナミクスはほぼ学習していることは分かったが、 どの点まで正確に学習しているかが分からないので前に方法で述べたグラフを描き考察する。
学習直後の教師信号をネットワークに初期値として与えた時のネットワークの出力と、 教師信号との距離の誤差を累計しグラフにしたものが図5.8である。
グラフを見ると二つの点に気付く。 まず一つは、 n=10000 の場合は学習がしっかり行なわれていないことが図5.3より明らかなので線の立ち上がりが早いのは分かるが、 n=100000 の線の立ち上がりが非常に早いということである。 これは、 少ない学習回数でも式のダイナミクスはほぼ学習できるが、 点を正確に描くということはできないということを意味している。 つまり図5.4は右側の教師信号の図とかなり近いように見えるが実は全く別の道をたどっているということになる。 もう一つは、 n=5000000 の方が n=10000000 よりも立ち上がりが遅く、 より正確な点を多く学習しているということである。 この理由ははっきりしていないが、 学習回数をある程度多くするとネットワークはどの入力が来ても無難な出力を出すようになってしまうのではないかと推測する。 すなわち、 どんな入力が来てもぴったりと教師信号に近付けようとはせず、 すべての入力に対して誤差がある程度小さくなるような出力を出すようにネットワークの重み、しきい値が固定されてしまうのではないだろうか、と考えたのである。
以上の実験の結果をまとめると、 バックプロパゲーション法を使うとニューラルネットワークに差分方程式のダイナミクスを学習させることはほぼ可能であるといえるが、 完璧には学習させることができず、 せいぜい正確に学習できるのは 20 点ほどである。 しかしアトラクタの点を完璧に学習させることよりも、 式のダイナミクスを学習させることが目的なので、 それが可能であったことは大きな研究成果である。
さらにこの結果は、 昨年大野宏氏が別のアルゴリズム [8] で同じエノン写像をニューラルネットワークに学習させた結果よりも多少誤差が小さく、 正確であった。 またバックプロパゲーション法の方がアルゴリズムが簡単であり、 学習させるプログラムもかなり短くなったので、 このような学習には適していると考えられる。
)