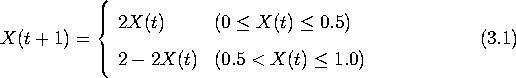
カオス（chaos）という単語は、日本語に訳せば 「混沌」や「無秩序」となる。 この言葉は近年、科学用語としても用いられるようになった。 小数自由度の決定論に従う、いわゆるノイズを含まない力学系における カオスと呼ばれる現象が、科学や工学などの諸分野に大きな波紋を広げつつある。
カオスとは決定論に従う力学系の解が初期値に鋭敏に依存する 予測不可能な振舞いを示し、そのアトラクタとしての次元が、 非線形のフラクタル次元となる現象である。 カオス現象は、自然物、人工物を問わず非線形システムに極当然に生じている。 風に吹かれて揺れる木の葉、海岸にうちよせる波など 日常で観察できる現象にもカオスは潜んでいる。 ラグビーボールが何回かのバウンド後に、 突然方向を変える現象もカオスの一例であるといえる。
カオスの定義は様々な研究者によってなされているが、 それらを総じて要約すると、 カオスとは、
「決定論的なシステムがつくり出す非周期振動」
実際にカオスの例を示す。
式（3.1）は、 第 t+1 項 X(t+1) の値が第 t 項 X(t) の値によって定まる 一般に１次元写像と呼ばれる数列である。
この系の入出力特性は図(3.1)の様になる。 この写像はテント写像と呼ばれる。
カオスの特徴を見るためにこの系に実際に初期値を与えて振舞いを観察してみる。
初期値として0.123456と0.123457を 
として代入し,
横軸を t ,
縦軸を X(t) としてプロットしグラフを描く。
のグラフを図(3.2)、
のグラフを図(3.3)に示す。
この二つのグラフを見ると、
始めの数点は似たような振舞いをするが、
t=20 のあたりから突如振舞いに変化がみられる。
カオスはこのように初期値に鋭敏に反応するという特徴をもつ。
これは図(3.1)を見ると分かるように、
同じ X(t+1) を与える X(t) が二つ存在するため、
グラフの平均的な勾配が急であるからである。
よって非常に近い二つの初期値を持っていたとしても
その振舞いは互いに急に離れていく。
このことは図(3.2)、図(3.3)を見ても明らかである。
乱れのないカオス系においては、 写像と初期値が与えられれば先の値は予測できるため、 先ほどの初期値鋭敏性はさほど問題ではない。 しかし自然界のように常に雑音、乱れの存在する系においては、 小さな乱れであっても鋭敏に反応するため予測ができなくなってしまう。 この（カオス＋小さな乱れ）の系が、本来は決定論的に定まるカオスを 実質的に非決定論的存在にしてしまっているのである。
以上に述べたカオスの特徴をまとめると次のようになる。
