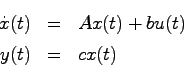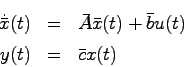: 可制御正準形,可観測正準形(多入力多出力)
: 同値変換
: 可制御正準形(1入力)
1入力システムの可制御正準形と同様、可観測な1出力システムの可観測正準形については、システムの可観測性行列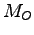 の正則性を用いる。したがって変換行列として
の正則性を用いる。したがって変換行列として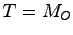 を直接利用する方法も考えられるが、教科書では変換行列として
を直接利用する方法も考えられるが、教科書では変換行列として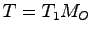 を利用している。この変換行列
を利用している。この変換行列 について以下の定理が成り立つ。なお、証明については可制御正準形と同様であるので、各自で試みること。
について以下の定理が成り立つ。なお、証明については可制御正準形と同様であるので、各自で試みること。
定理(1入力1出力システムの可観測正準形)可観測な1入力1出力システム
は,次のシステムに同値である.
ただし,
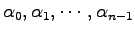 は,
は, の特性多項式の係数であり,
の特性多項式の係数であり,
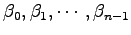 は適当な実数である.
は適当な実数である.
h本小節の前書きにも書いたが、具体的にシステムの状態方程式が与えられたとき,可観測正準形(25.10),(25.11)に変換するための変換行列を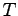 とすると,
とすると,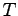 は一般的に次の方法で求められる.
は一般的に次の方法で求められる.
方法
さらに次の定理が成り立つ.
定理 与えられたシステムに対する可観測正準系
と可観測正準形
の間には次の関係がある.
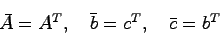 |
(8.30) |
endo
平成16年6月30日
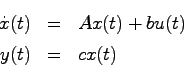
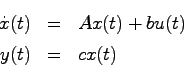
![]() とすると,
とすると,![]() は一般的に次の方法で求められる.
は一般的に次の方法で求められる.