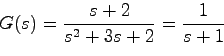| (8.7) | |||
| (8.8) |
本小節では与えられたシステムに対し,同値変換をすることでシステムを可制御正準形,可観測正準形と呼ばれるある種の標準的なシステム表現に変換する.なお,可制御正準系はシステムの極の設定や最適制御を求める際に用いられる.また,可観測正準形は状態オブザーバやカルマンフィルタなどの構成に用いられる.
以下ではシステム
システム(8.7),(8.8)は可制御であるから、可制御性行列
![$M_C = \left[ \begin{array}{cccc}b & Ab & \cdots & A^{n-1}b \end{array}\right]$](img310.png) は
は![]() 次の正則行列であるから、これを使った変換行列としては
次の正則行列であるから、これを使った変換行列としては
![]() の2種類が候補となる。それぞれについて調べてみる。
の2種類が候補となる。それぞれについて調べてみる。
![\begin{eqnarray*}
T^{-1} \tilde{b} &=& b \\
M_C \tilde{b} &=& b \\
\left[ \begin{array}{cccc} b & Ab & \cdots & A^{n-1}b \end{array}\right] &=& b
\end{eqnarray*}](img317.png)
(8.10)式より
![]() なので
なので
後述するように、教科書では![]() ではなく、
ではなく、![]() を係数行列に採用している。このことは特に重要ではないのだが、教科書と同様の表記にするためには、変換行列として
を係数行列に採用している。このことは特に重要ではないのだが、教科書と同様の表記にするためには、変換行列として![]() ではなく
ではなく
明らかに![]() は正則行列であるから
は正則行列であるから![]() は正則である。
は正則である。
以下、上記変換行列
![]() を利用することにより次の定理が得られる。
を利用することにより次の定理が得られる。
定理 (1入力1出力システムの可制御正準形) 可制御な1入力1出力システム
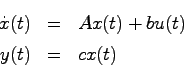
(証明)
![]() より
より
![$T^{-1} = \left[ \begin{array}{ccc} t_1 & \cdots & t_n \end{array}\right]$](img344.png) とおけば(25.4)より
とおけば(25.4)より
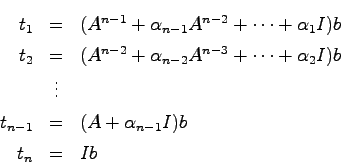
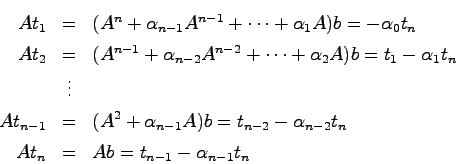
例3.6 次のシステムを考える:
このシステムの可制御性行列![]() は
は
![\begin{displaymath}
M_c = \left[ \begin{array}{cc} 1 & -1 1 & -2 \end{array} \right]
\end{displaymath}](img357.png)
![\begin{displaymath}
\det[sI-A] = \det \left[ \begin{array}{cc}s+1 & 0 0 & s+2 \end{array}\right] = s^2 + 3s + 2
\end{displaymath}](img358.png)
![\begin{eqnarray*}
T &=& ( M_c T_1)^{-1} \\
& = & \left( \left[ \begin{array}{cc...
...
&=& \left[ \begin{array}{cc}1 & -1 -1 & 2 \end{array}\right]
\end{eqnarray*}](img359.png)
したがって,このシステムの可制御正準形は
![\begin{eqnarray*}
\dot{\bar{x}}(t) &=& TAT^{-1}\bar{x}(t) + Tbu(t) \\
&=& \left...
...
&=& \left[\begin{array}{cc}2 & 1 \end{array}\right] \bar{x}(t)
\end{eqnarray*}](img360.png)
また,例2.7で示したように,このシステムの伝達関数は