可制御正準形，可観測正準形（多入力多出力）

本小節では前節で与えた１入力１出力システムの可制御正準形，可観測正準形を拡張し，多入力多出力システムの可制御正準形，可観測正準形を求める．そのため，まず可制御性指数と呼ばれるものについて定義を行なう．  

可制御性指数　多入力システム$(A,B,C)$を考える．ただし，$A,B,C$はそれぞれ $n \times n,n \times m, r \times n$定数行列とする．さらに，入力$u(t)$の係数行列$B$が$m$個の列ベクトル$b_i$により $B = [b_1 \;\; b_2 \;\; \cdots \;\;b_m]$と表されるものとする．このシステムに対し

$$\mu_i := \min\{ j\;\vert\;A^jb_i \in {\rm span}\left[ \begin... ... & A^{j-1}B & A^jb_1 & \cdots & A^jb_{i-1}\end{array}\right]\}$$ (8.31)

と定義し，これを可制御性指数と呼ぶ．  

可制御性指数により，多入出力システムの可制御性準形を求める前に，可制御性指数を具体的に計算してみる．  

例3.7　行列$A,B$を

$$A = \left[ \begin{array}{ccccc} 1 & 0 & 1 & 0 & 1 \\ 0 & 0 ... ... 0 & 0 1 & 0 0 & 1 1 & 0 0 & -1 \end{array}\right]$$

とすると，

$$\begin{eqnarray*} \lefteqn{\left[ \begin{array}{ccccc} B & AB & A^2B & A^3B & A^... ...* \\ 0 & -1 & 0 & 1 & 1 & -2 & 0 & * & * & * \end{array}\right] \end{eqnarray*}$$

となり，

$$\begin{eqnarray*} A^3b_1 &=& 4b_1 + 4b_2 + 0Ab_1 + 2Ab_2 + 2A^2b_1 + 0A^2b_2 \\ A^2b_2 &=& 0b_1 + 0b_2 - 1Ab_1 - 1Ab_2 - 1A^2b_1. \end{eqnarray*}$$

したがって， $\mu_1 = 3,\;\mu_2 = 2$となる．  

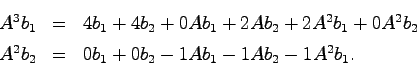
次に，上記の可制御性指数を用いて，多入力システムを可制御正準形に変形する方法について述べる．なお多入力システムの可制御正準形とは，システムの状態変数をいくつかのブロックに分けたとき，ブロックごとに可制御正準形システムが構成されるよう同値変換を施したシステムである．  

定理　多入力システム$(A,B,C)$が可制御であり，行列$B$が最大の階数を持てば，すなわち ${\rm rank}B = m$であれば，可制御正準形 $(\tilde{A},\tilde{B},\tilde{C})$に変換できる．ただし，

$$\tilde{A} = \left[ \begin{array}{ccc} \tilde{A}_{11} & \cdot... ...y}{c} \tilde{B}_1 \vdots \tilde{B}_m \end{array} \right]$$ (8.32)

であり， $\tilde{A}_{ij}$および$\tilde{B}_i$はそれぞれ

$$\tilde{A}_{ii} =$$ (8.33)

$$\tilde{A}_{ij} =$$ (8.34)

$$\tilde{B}_{i} =$$ (8.35)

で与えられる．また，$\tilde{C}$は適当な行列である．  

具体的にシステムの状態方程式が与えられたときに，課制御正準形式(25.9)〜(25.11)へ変換するための変換行列を$T$とすると，$T$は一般に次の方法で求められる．  

多入力システムの可制御正準形式への変換　与えられたシステム$(A,B,C)$に対し，行列$S$を次式で定義する．

$$S = \left[ \begin{array}{ccccccccc} b_1 & Ab_1 & \cdots & A^... ...A^{\mu_2 -1}b_2 & \cdots & A^{\mu_m -1}b_m \end{array}\right].$$ (8.36)

これに対し，$S$の逆行列の第 $(\sum_{j=1}^i \mu_j)$行目を$\hat{s}_i$とし，

$$T = \left[ \begin{array}{c} \hat{s}_1 \hat{s}_1A \\ \vdo... ...t{s}_2 \vdots \\ \hat{s}_m A^{\mu_m -1} \end{array}\right]$$ (8.37)

と置けばよい．  

例3.8　例3.7のシステムに対し，可制御正準形を求める．まず行列$S$は

$$S= \left[ \begin{array}{ccccc} 0 & 0 & 1 & 0 & 0 \\ 1 & 0 &... ... 1 & -1 & 0 & 0 & -1 \\ 0 & 0 & 1 & -1 & 1 \end{array}\right]$$ (8.38)

となる．ゆえに

$$S^{-1} = \left[ \begin{array}{ccccc} 3 & 2 & -1 & -1 & -1 \\... ...& 1 & -1 & -1 & -2 \\ 2 & 1 & -1 & -1 & -1 \end{array}\right]$$ (8.39)

であるから

$$\begin{eqnarray*} \hat{s}_1 &=& \left[ \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \e... ...t[ \begin{array}{ccccc} 2 & 1 & -1 & -1 & -1 \end{array}\right]. \end{eqnarray*}$$

したがって，

$$T = \left[ \begin{array}{c} \hat{s}_1 \hat{s}_1 A \hat... ... & 1 & -1 & -1 & -1 \\ 3 & 0 & 0 & 0 & -1 \end{array}\right].$$

また，

$$T^{-1} = \left[ \begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ -... ... 2 & -3 & 1 & -1 & 1 \\ 3 & 0 & 0 & 0 & -1 \end{array}\right]$$

となる．これより可制御正準形が得られる．ただし

$$\bar{A} = TAT^{-1} = \left[ \begin{array}{ccc\vert cc} 0 & 1... ... 0 & 0 1 & -1 \hline 0 & 0 0 & 1 \end{array}\right]$$

および $\bar{C} = CT^{-1}$である．  

１入力システムの可制御正準形は一意に求めれるが，多入力システムにおける可制御正準形は一意には求められない．このことは次に示す例により判る．  

例3.9　可制御正準形で与えられるシステム

$$\dot{\bar{x}}(t) = \left[ \begin{array}{ccc} 0 & 1 & 0 -1... ...egin{array}{cc} 0 & 0 1 & 1 0 & 1 \end{array}\right]u(t)$$ (8.40)

に対して，いま$t_{31}$を任意の実数として

$$T = \left[ \begin{array}{ccc} 1 & 0 & 0 0 & 1 & 0 t_{31} & 0 & 1 \end{array}\right]$$

という同値変換を考えると，別な形の可制御正準形

$$\dot{\bar{x}}(t) = \left[ \begin{array}{ccc} 0 & 1 & 0 -1... ...egin{array}{cc} 0 & 0 1 & 1 0 & 1 \end{array}\right]u(t)$$

が得られる．したがって多入力システム(26.4)に同値なシステムの可制御正準系は一意でなく，無限個存在する．  

可観測性指数　可制御性指数と同様にして，可観測性指数が定義される：
多入力システム$(A,B,C)$を考える．ただし，$A,B,C$はそれぞれ $n \times n,n \times m, r \times n$定数行列とする．さらに，$C$が$r$個の行ベクトル$c_i$によって $C=\left[ \begin{array}{ccccc}c_1^T & c_2^T & \cdots & c_r^T \end{array}\right]^T$ と表されるものとする．このシステムに対し

と定義し，これを可観測性指数と呼ぶ．  

定理　多入力システム$(A,B,C)$が可観測であり，行列$C$が最大ランクを持てば，すなわち${\rm rank}C=r$であれば，そのシステムは可観測正準形 $(\bar{A},\bar{B},\bar{C})$に変換できる．ただし，

$$\bar{A} = \left[ \begin{array}{ccc} \bar{A}_{11} & \cdots & ... ...{array}{ccc} \bar{C}_1 & \cdots & \bar{C}_r \end{array}\right]$$

であり，$\bar{A}_{ij}$及び$\bar{C}_i$はそれぞれ

で与えられる．