


: 線形関数オブザーバ
: sysconh16
: 同一次元状態オブザーバ
推定したい状態変数は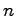 次元であり,利用可能な出力が
次元であり,利用可能な出力が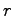 次元であるから,
一般に状態オブザーバの次元数は
次元であるから,
一般に状態オブザーバの次元数は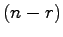 以上でなければその機能を発揮できない.
このことから
以上でなければその機能を発揮できない.
このことから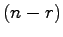 次元状態オブザーバを最小次元状態オブザーバと呼ぶ.
本節ではこの最小次元状態オブザーバの一つの構成法を与える.
次元状態オブザーバを最小次元状態オブザーバと呼ぶ.
本節ではこの最小次元状態オブザーバの一つの構成法を与える.
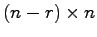 行列
行列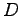 を適当に選び,
を適当に選び,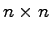 行列
行列
![\begin{displaymath}
T = \left[ \begin{array}{c}C D \end{array}\right]
\end{displaymath}](img1046.png) |
(25.1) |
が正則となるようにする.この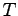 を用いて
を用いて
なる変換を行なえば
となる.ただし
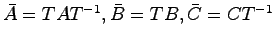 である.
また(25.1)式より
である.
また(25.1)式より
であるから
![\begin{displaymath}
\bar{C} = \left[ \begin{array}{cc}I_r & 0\end{array}\right]
\end{displaymath}](img1053.png) |
(25.4) |
であることが示せる.
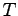 が
が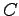 と
と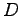 に分かれていることに応じて,次のように
に分かれていることに応じて,次のように
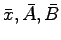 を分割する.
を分割する.
![\begin{displaymath}
\bar{x} = \left[ \begin{array}{c}\bar{x}_1 \bar{x}_2 \end...
...eft[ \begin{array}{c}\bar{B}_1 \bar{B}_2 \end{array}\right]
\end{displaymath}](img1055.png) |
(25.5) |
すると
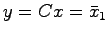 であることから(25.2)式は
であることから(25.2)式は
と書き換えられる.いま仮に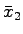 を状態変数とするシステムを考え,
(25.6)式が状態方程式,(25.7)が出力方程式であると見なす.すなわち
を状態変数とするシステムを考え,
(25.6)式が状態方程式,(25.7)が出力方程式であると見なす.すなわち
ただし
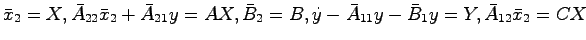 である.
すると,
である.
すると,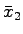 に対する同一次元状態オブザーバは,(8.13)式より
に対する同一次元状態オブザーバは,(8.13)式より
となる.ここで(25.8)式の右辺に存在する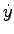 の項を消去するために
の項を消去するために
の変数変換を行なえば,(25.8)式は
となる.また(25.9)式の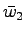 は,
は,
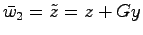 と表されるから,
と表されるから,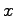 の推定値
の推定値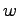 は
は
![\begin{displaymath}
w = \left[ \begin{array}{c}x_1 w_2 \end{array}\right]
= T...
...}\left[ \begin{array}{c}y z+Gy \end{array}\right] (= Wz+Vy)
\end{displaymath}](img1074.png) |
(25.11) |
によって与えられる.ただし
![\begin{displaymath}
W=T^{-1}\left[ \begin{array}{c} 0 I_{n-r} \end{array}\rig...
...d
V= T^{-1}\left[ \begin{array}{c} I_r G \end{array}\right]
\end{displaymath}](img1075.png) |
(25.12) |
である.よって,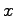 に対する
に対する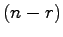 次元状態オブザーバは,(25.10),(25.11)式で与えられる.
次元状態オブザーバは,(25.10),(25.11)式で与えられる.
なお,対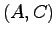 が可観測ならば,対
が可観測ならば,対
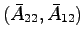 も可観測であることが示せるので,適当な
も可観測であることが示せるので,適当な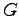 を選ぶことによって,オブザーバの極,すなわち
を選ぶことによって,オブザーバの極,すなわち
![$[\bar{A}_{22}-G\bar{A}_{12}]$](img1077.png) の固有値を任意に設定できる.
の固有値を任意に設定できる.
以上の結果より,次の手順によって,一つの最小次元オブザーバ(25.10),(25.11)が得られる.
-
![$T=\left[ \begin{array}{cc}C & D\end{array}\right]^{T}$](img1078.png) が正則となる
が正則となる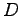 の
決定
の
決定
-
![$\displaystyle{\bar{A} = TAT^{-1} = \left[ \begin{array}{cc}
\bar{A}_{11} & \bar{A}_{12} \bar{A}_{21} & \bar{A}_{22} \end{array}\right]}$](img1079.png) による
による
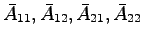 の算出
の算出
-
![$[\bar{A}_{22}-G\bar{A}_{12}]$](img1077.png) の固有値が,目標通りになる
の固有値が,目標通りになる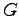 の決定
の決定
- (25.12)式による
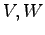 の計算と,(25.10)の係数行列の計算
の計算と,(25.10)の係数行列の計算
例7.2 例7.1のシステム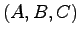 に対して,最小次元状態オブザーバを,その極が
に対して,最小次元状態オブザーバを,その極が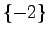 となるように設計する.
となるように設計する.
システムは
より,
ととると,
より,
![$\bar{A} = A, \bar{B}=\left[ \begin{array}{cc}1 & 1 \end{array}\right]^T$](img1085.png) となる.
これより
となる.
これより
![$[\bar{A}_{22}-G\bar{A}_{12}]=1-G=-2$](img1086.png) を満たす
を満たす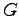 として
として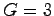 が得られる.
よって,オブザーバは次式のようになる.
が得られる.
よって,オブザーバは次式のようになる.
なお,最小次元状態オブザーバ(25.10),(25.11)は,
![$U=[-GI_{n-r}]T$](img1089.png) ととるとき,
ととるとき,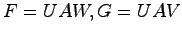 と表せることと,(25.12)を用いれば,定理7.1を満たすことが確かめられる.
と表せることと,(25.12)を用いれば,定理7.1を満たすことが確かめられる.
演習問題7.2 システム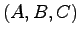 を考える.ただし
を考える.ただし
とする.このシステムに対して最小次元状態オブザーバを,その極が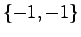 となるように設計せよ.
となるように設計せよ.
(解答例)
とすると
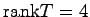 より
より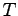 は正則となる.これより
は正則となる.これより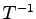 を求めると
を求めると
であるから
となる.次に
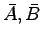 を求めると
を求めると
となる.
![$G = \left[ \begin{array}{cc}g_{11} & g_{12} g_{21} & g_{22}
\end{array}\right]$](img1099.png) と置き,
と置き,
![$[\bar{A}_{22}-G\bar{A}_{12}]$](img1077.png) の固有値が
の固有値が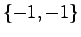 となるように設定する:
となるように設定する:
であるから
したがって,
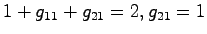 となり,結局
となり,結局
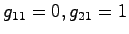 である.
よって,題意を満たす
である.
よって,題意を満たす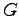 の一つとして
の一つとして
が選べる.
以上により,最小次元オブザーバの状態方程式は
となり,出力方程式は
となる.



: 線形関数オブザーバ
: sysconh16
: 同一次元状態オブザーバ
endo
平成16年6月30日
![]() 次元であり,利用可能な出力が
次元であり,利用可能な出力が![]() 次元であるから,
一般に状態オブザーバの次元数は
次元であるから,
一般に状態オブザーバの次元数は![]() 以上でなければその機能を発揮できない.
このことから
以上でなければその機能を発揮できない.
このことから![]() 次元状態オブザーバを最小次元状態オブザーバと呼ぶ.
本節ではこの最小次元状態オブザーバの一つの構成法を与える.
次元状態オブザーバを最小次元状態オブザーバと呼ぶ.
本節ではこの最小次元状態オブザーバの一つの構成法を与える.
![]() 行列
行列![]() を適当に選び,
を適当に選び,![]() 行列
行列
![\begin{displaymath}
\left[ \begin{array}{cc} I_r & 0 \end{array}\right] T =
\le...
...}\right] \left[ \begin{array}{c}
C D \end{array}\right] = C
\end{displaymath}](img1052.png)
![]() が
が![]() と
と![]() に分かれていることに応じて,次のように
に分かれていることに応じて,次のように
![]() を分割する.
を分割する.
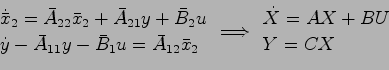
![]() が可観測ならば,対
が可観測ならば,対
![]() も可観測であることが示せるので,適当な
も可観測であることが示せるので,適当な![]() を選ぶことによって,オブザーバの極,すなわち
を選ぶことによって,オブザーバの極,すなわち
![]() の固有値を任意に設定できる.
の固有値を任意に設定できる.
![]() に対して,最小次元状態オブザーバを,その極が
に対して,最小次元状態オブザーバを,その極が![]() となるように設計する.
となるように設計する.
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}1 & 1 0 & 1 \end{array}...
...]u,\quad
y = \left[ \begin{array}{cc}1 & 1\end{array}\right] x
\end{displaymath}](img1039.png)
![\begin{displaymath}
T = \left[ \begin{array}{c}C D \end{array}\right] = \left[ \begin{array}{cc}
1 & 1 0 & 1 \end{array}\right]
\end{displaymath}](img1083.png)
![\begin{displaymath}
T^{-1} = \left[ \begin{array}{cc}
1 & -1 0 & 1 \end{array}\right]
\end{displaymath}](img1084.png)
![$\bar{A} = A, \bar{B}=\left[ \begin{array}{cc}1 & 1 \end{array}\right]^T$](img1085.png) となる.
これより
となる.
これより
![\begin{eqnarray*}
\dot{z} &=& -2z-9y-2u \\
w &=& \left[ \begin{array}{c}-1 1...
...}\right]z + \left[ \begin{array}{c}-2 3 \end{array}\right] y
\end{eqnarray*}](img1088.png)
![]() ととるとき,
ととるとき,![]() と表せることと,(25.12)を用いれば,定理7.1を満たすことが確かめられる.
と表せることと,(25.12)を用いれば,定理7.1を満たすことが確かめられる.
![]() を考える.ただし
を考える.ただし
![\begin{displaymath}
A = \left[ \begin{array}{cccc}0 & 0 & 0 & 1 1 & 0 & 0 & 0...
...{array}{cccc}1 & 1 & 0 & 0 0 & 1 & 1 & 0 \end{array}\right]
\end{displaymath}](img1091.png)
![\begin{displaymath}
T = \left[ \begin{array}{c}C D \end{array}\right]
= \left...
... & 1 & 0 \\
0 & 0 & 1 & 0 0 & 0 & 0 & 1 \end{array}\right]
\end{displaymath}](img1093.png)
![\begin{eqnarray*}
\left[ \begin{array}{cccc\vert cccc}1 & 1 & 0 & 0 & 1 & 0 & 0 ...
... 0 & 1 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \end{array}\right]
\end{eqnarray*}](img1096.png)
![\begin{displaymath}
T^{-1} = \left[ \begin{array}{cccc}
1 & -1 & 1 & 0 0 & 1 & -1 & 0 0 & 0 & 1 & 0 0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img1097.png)
![\begin{eqnarray*}
\bar{A} = TAT^{-1}
&=& \left[ \begin{array}{cc\vert cc}1 & -1...
...eft[ \begin{array}{c} 0 0 \hline 0 1 \end{array}\right]
\end{eqnarray*}](img1098.png)
![$G = \left[ \begin{array}{cc}g_{11} & g_{12} g_{21} & g_{22}
\end{array}\right]$](img1099.png) と置き,
と置き,
![\begin{displaymath}
\bar{A}_{22}-G\bar{A}_{12} = \left[ \begin{array}{cc} -1-g_{11} & -g_{11} \\
-g_{21} & -g_{21} \end{array}\right]
\end{displaymath}](img1100.png)
![\begin{displaymath}
\det[sI-(\bar{A}_{22}-G\bar{A}_{12})] = \det \left[ \begin{a...
...g_{21} \end{array}\right]
= s^2 + (1+g_{11}+g_{21})s + g_{21}.
\end{displaymath}](img1101.png)
![\begin{displaymath}
G = \left[ \begin{array}{cc}0 & 0 1 & 0 \end{array}\right]
\end{displaymath}](img1104.png)
![\begin{eqnarray*}
\dot{\tilde{z}} &=& [ \bar{A}_{22}-G\bar{A}_{12}]z +
[\bar{A}...
...ray}\right]y
+ \left[ \begin{array}{c}0 1\end{array}\right]u
\end{eqnarray*}](img1105.png)
![\begin{eqnarray*}
w = Wz+Vy
&=& T^{-1}\left[ \begin{array}{c} 0 I_{n-r} \end...
...{array}{cc}1 & -1 0 & 1 0 & 0 1 & 0 \end{array}\right]u
\end{eqnarray*}](img1106.png)