線形関数オブザーバの必要性は,通常状態変数![]() が直接観測できないとき,オブザーバによる推定値
が直接観測できないとき,オブザーバによる推定値![]() を用いて線形フィードバック則
を用いて線形フィードバック則![]() を
を![]() で代用することが行なわれる.このような目的でオブザーバを用いる場合には必ずしも
で代用することが行なわれる.このような目的でオブザーバを用いる場合には必ずしも![]() そのものを推定する必要はなく,フィードバック則
そのものを推定する必要はなく,フィードバック則![]() の推定値を求めればよいことがわかる.また,その場合
の推定値を求めればよいことがわかる.また,その場合![]() の値は前節で述べた最小次元状態オブザーバよりもさらに低い次数のオブザーバで推定できることが多い.
の値は前節で述べた最小次元状態オブザーバよりもさらに低い次数のオブザーバで推定できることが多い.
このようなことから以下では![]() を
を![]() 行列
行列![]() とする.(8.3),(8.4)すなわち
とする.(8.3),(8.4)すなわち
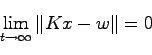
定理7.3 ![]() 次元システム(26.1),(26.2)は,その係数行列
次元システム(26.1),(26.2)は,その係数行列
![]() が次の条件を満たすとき,システム(8.1),(8.2)に対
して
が次の条件を満たすとき,システム(8.1),(8.2)に対
して![]() を推定する線形関数オブザーバである.
を推定する線形関数オブザーバである.
証明 定理7.1の条件と異なるのは(26.5)のみであるから,定理7.1の証明中の式(8.9)まではそのまま成立する.さらに式(8.2),(26.2),(26.5)より
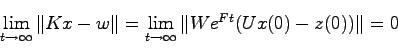
例7.3 例7.1のシステム
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}1 & 1 0 & 1 \end{array}...
...]u,\quad
y = \left[ \begin{array}{cc}1 & 1\end{array}\right] x
\end{displaymath}](img1039.png)
![$-\left[ \begin{array}{cc}5 & 4 \end{array}\right]x$](img1123.png) を推定し,その極が
を推定し,その極が
まず![]() 及び
及び
![$w=-\left[ \begin{array}{cc}5 & 4 \end{array}\right]x$](img1125.png) より線形オブザーバ
より線形オブザーバ
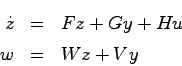
次にオブザーバの極が![]() であるためには
であるためには![]() でなければならない.
でなければならない.
さらに![]() を
を
![$U=\left[ \begin{array}{cc} u_1 & u_2 \end{array}\right]$](img1127.png) とおくと,(26.3),(26.4),(26.5)より
とおくと,(26.3),(26.4),(26.5)より
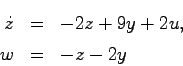
演習問題1 システム
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}1 & 0 -2 & 1 \end{array...
...]u,\quad
y = \left[ \begin{array}{cc}1 & 1 \end{array}\right]x
\end{displaymath}](img1135.png)
![$\left[ \begin{array}{cc}1 & -5\end{array}\right]x$](img1136.png) を推定し,極が
を推定し,極が
(解) まず![]() 及び
及び
![$w = \left[ \begin{array}{cc}1 & -5\end{array}\right]x$](img1138.png) より線形関数オブザーバの係数行列はすべてスカラーである.
より線形関数オブザーバの係数行列はすべてスカラーである.
さらにオブザーバの極が![]() であることから
であることから![]() となる.
次に
となる.
次に
![$U=\left[ \begin{array}{cc} u_1 & u_2 \end{array}\right]$](img1127.png) とおくと
とおくと
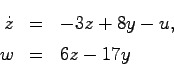
演習問題2 システム
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}2 & 0 0 & -2 \end{array...
...]u,\quad
y = \left[ \begin{array}{cc}1 & 1 \end{array}\right]x
\end{displaymath}](img1144.png)
![$\left[ \begin{array}{cc}-17/4 & 1/4\end{array}\right]x$](img1145.png) を推定し,極が
を推定し,極が