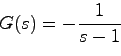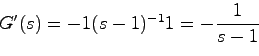: 実現問題
: sysconh16
: 正準変換
1入力1出力の線形システム
に対し,ラプラス変換により伝達関数 が
が
で求められることは既に示した.
本節の目的は,上記の考え方を多入力多出力システムに拡張することにある.
以下のシステムを考える:
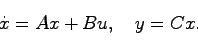 |
(11.1) |
ここで状態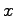 ,入力
,入力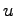 ,出力
,出力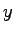 はそれぞれ
はそれぞれ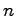 次,
次,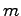 次,
次,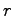 次列ベクトルであるとする.すなわち係数行列
次列ベクトルであるとする.すなわち係数行列 は
は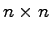 行列,
行列,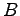 は
は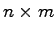 行列,
行列,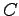 は
は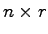 行列である.
(11.1)式をラプラス変換し,入力
行列である.
(11.1)式をラプラス変換し,入力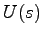 と出力
と出力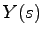 の比
の比 を求めると,
を求めると,
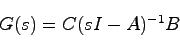 |
(11.2) |
である.念のため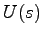 は,
は,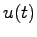 を
を
![$u(t) = \left[\begin{array}{cccc}u_1(t) & u_2(t) & \cdots & u_m(t)\end{array}\right]^T$](img585.png) としたときの各成分ごとのラプラス変換を表す:
としたときの各成分ごとのラプラス変換を表す:
したがって,(11.2)式で求められる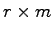 行列
行列 を
を
![\begin{displaymath}
G(s) = \left[ \begin{array}{ccc}
g_{11}(s) & \cdots & g_{1m}...
...& \vdots \\
g_{r1}(s) & \cdots & g_{rm}(s)
\end{array}\right]
\end{displaymath}](img588.png) |
(11.3) |
とすると,各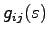 は入力の第
は入力の第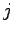 要素
要素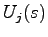 から出力の第
から出力の第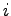 要素
要素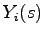 への伝達関数を表すものと考えられる.このことから
への伝達関数を表すものと考えられる.このことから を伝達関数行列と呼ぶ.
を伝達関数行列と呼ぶ.
定理4.1 互いに同値なシステムに対する伝達関数行列は,すべて等しい.
(証明)同値変換のところで既に証明済み.
定理4.2 システム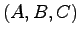 の伝達関数行列
の伝達関数行列 は,システムのカルマン正準分解における可制御,可観測なサブシステムの係数行列
は,システムのカルマン正準分解における可制御,可観測なサブシステムの係数行列
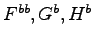 によって
によって
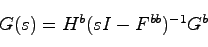 |
(11.4) |
と表される.
(証明) 前節の定理からシステム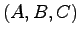 のカルマン正準分解
のカルマン正準分解
に対し,逆行列の公式
を使い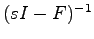 を求める.このため
を求める.このため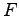 を次のようにブロック化しておく:
を次のようにブロック化しておく:
これにより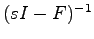 は
は
ここで
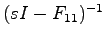 は
は
であるから(
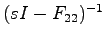 も同様),
も同様),
となる.ここで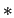 は特に値を必要としないのでこのようにあらわす.
は特に値を必要としないのでこのようにあらわす.
よって
となる.
以上の定理からシステムの伝達関数行列は,その可制御可観測なサブシステムが同値であれば,他のサブシステムがどんなに異なっていようと同じ伝達関数行列を持つ.
例4.1 例3.10に対して, が
が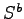 の特性を表していることを確かめる.正準分解形
の特性を表していることを確かめる.正準分解形
より は
は
となる.他方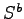 の伝達関数行列
の伝達関数行列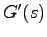 は,教科書p.61式(3.61),(3.62)より
は,教科書p.61式(3.61),(3.62)より
であり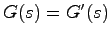 である.
である.



: 実現問題
: sysconh16
: 正準変換
endo
平成16年6月30日
![$u(t) = \left[\begin{array}{cccc}u_1(t) & u_2(t) & \cdots & u_m(t)\end{array}\right]^T$](img585.png) としたときの各成分ごとのラプラス変換を表す:
としたときの各成分ごとのラプラス変換を表す:
![\begin{displaymath}
U(s) = \left[ \begin{array}{cccc} U_1(s) & U_2(s) & \cdots & U_m(s)\end{array}\right]^T.
\end{displaymath}](img586.png)
![]() の伝達関数行列
の伝達関数行列![]() は,システムのカルマン正準分解における可制御,可観測なサブシステムの係数行列
は,システムのカルマン正準分解における可制御,可観測なサブシステムの係数行列
![]() によって
によって
![]() のカルマン正準分解
のカルマン正準分解
![\begin{eqnarray*}
F &=& \left[ \begin{array}{cccc}
F^{aa} & F^{ab} & F^{ac} & F^...
... \left[ \begin{array}{cccc}0 & H^b & 0 & H^d \end{array}\right].
\end{eqnarray*}](img595.png)
![\begin{displaymath}
\left[ \begin{array}{cc} A_{11} & A_{12} 0 & A_{22} \end{...
...}^{-1}A_{12}A_{22}^{-1} \\
0 & A_{22}^{-1} \end{array}\right]
\end{displaymath}](img596.png)
![\begin{displaymath}
F = \left[ \begin{array}{cc\vert cc} F^{aa} & F^{bb} & F^{ac...
...n{array}{cc} F_{11} & F_{12} 0 & F_{22}
\end{array}\right].
\end{displaymath}](img599.png)
![\begin{eqnarray*}
(sI-F)^{-1} &=& \left[ \begin{array}{cc}
sI-F_{11} & -F_{12} \...
...}(sI-F_{22})^{-1} \\
0 & (sI - F_{22})^{-1} \end{array}\right].
\end{eqnarray*}](img600.png)
![\begin{eqnarray*}
(sI-F_{11})^{-1} &=& \left[ \begin{array}{cc}
sI-F^{aa} & -F^{...
...{ab}(sI-F^{bb})^{-1} \\
0 & (sI-F^{bb})^{-1} \end{array}\right]
\end{eqnarray*}](img602.png)
![\begin{displaymath}
(sI-F)^{-1}=\left[ \begin{array}{cccc}
(sI-F^{aa})^{-1} & * ...
...^{-1} & * \\
0 & 0 & 0 & (sI-F^{dd})^{-1}
\end{array}\right]
\end{displaymath}](img604.png)
![\begin{eqnarray*}
G(s) &=& \left[ \begin{array}{cccc} 0 & H^b & 0 & H^d \end{arr...
... G^b 0 0 \end{array}\right] \\
&=& H^b(sI-F^{bb})^{-1}G^b
\end{eqnarray*}](img606.png)
![]() が
が![]() の特性を表していることを確かめる.正準分解形
の特性を表していることを確かめる.正準分解形
![\begin{displaymath}
\dot{\bar{x}} = \left[ \begin{array}{cccc}-1 & 1 & 1 & 0 ...
...t[ \begin{array}{cccc}0 & 1 & 0 & 1 \end{array}\right]
\bar{x}
\end{displaymath}](img577.png)