


: 最小実現
: sysconh16
: 伝達関数行列(後期第1回)
前節においてシステムの状態方程式表現が与えられたとき,その伝達関数(行列)表現は一意に与えられることを示した.本節ではその逆の問題,すなわち伝達関数(行列)表現が与えられた場合に,その状態方程式表現を求める問題を考える.
この問題は,状態方程式表現が求められれば,積分器を用いた電気系などにより,ハードウェア回路として実現できるという意味で,実現問題と呼ばれる.
行列 の各要素が
の各要素が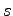 の有理関数であるとき(すなわち,分母および分子が
の有理関数であるとき(すなわち,分母および分子が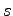 の多項式であるような分数の形をしているとき),
の多項式であるような分数の形をしているとき), を有理行列といい,さらに各要素が
を有理行列といい,さらに各要素が
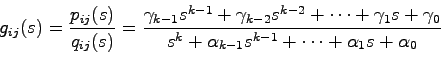 |
(12.1) |
のように(分母の次数)>(分子の次数)であるとき有理行列 は,厳密にプロパーであるという(
は,厳密にプロパーであるという(
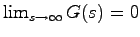 と定義しても良い).
と定義しても良い).
定理4.3 有理行列が実現可能であるための必要十分条件は,それが厳密にプロパーなことである.
(証明)まず必要性,すなわち有理行列が実現可能ならば厳密にプロパーであることを証明する.
 は実現可能であるから,
は実現可能であるから, の任意の実現をシステム
の任意の実現をシステム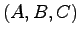 とし,その次元を
とし,その次元を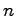 とする.前節の定理より明らかに
とする.前節の定理より明らかに
である.
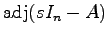 は
は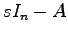 の余因子行列であるから,明らかに
の余因子行列であるから,明らかに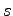 に関して
に関して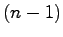 次以下になる.また
次以下になる.また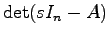 は
は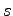 に関して
に関して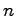 次になる.以上により
次になる.以上により は厳密にプロパーである.
は厳密にプロパーである.
次に十分性を示す.ここで前節で示したように, はシステムを正準分解した可制御可観測なサブシステムを用いて
はシステムを正準分解した可制御可観測なサブシステムを用いて
で表されることに注意する.
 が厳密にプロパーであれば,
が厳密にプロパーであれば, の一つの実現が存在することを示せばよい.
の一つの実現が存在することを示せばよい. の第
の第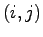 要素
要素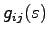 が(12.1)式で与えられるとすると,教科書図4.1より
が(12.1)式で与えられるとすると,教科書図4.1より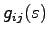 は入力
は入力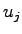 ,出力
,出力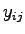 の1入力1出力システムの伝達関数と考えられる.したがって,
の1入力1出力システムの伝達関数と考えられる.したがって,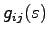 は定理3.4と教科書(3.49)式により
は定理3.4と教科書(3.49)式により
という,可制御正準形をした一つの実現を持つ.この実現は教科書図4.2で表される.したがって
とおけば,システム
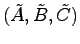 は,
は, の一つの実現である.このことはシステム
の一つの実現である.このことはシステム
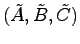 の伝達関数行列
の伝達関数行列
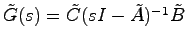 の第
の第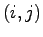 要素
要素
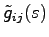 が
が
となることからも確かめられる.
endo
平成16年6月30日
![]() の各要素が
の各要素が![]() の有理関数であるとき(すなわち,分母および分子が
の有理関数であるとき(すなわち,分母および分子が![]() の多項式であるような分数の形をしているとき),
の多項式であるような分数の形をしているとき),![]() を有理行列といい,さらに各要素が
を有理行列といい,さらに各要素が
![]() は実現可能であるから,
は実現可能であるから,![]() の任意の実現をシステム
の任意の実現をシステム![]() とし,その次元を
とし,その次元を![]() とする.前節の定理より明らかに
とする.前節の定理より明らかに
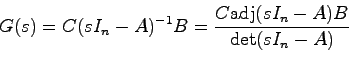
![]() はシステムを正準分解した可制御可観測なサブシステムを用いて
はシステムを正準分解した可制御可観測なサブシステムを用いて
![]() が厳密にプロパーであれば,
が厳密にプロパーであれば,![]() の一つの実現が存在することを示せばよい.
の一つの実現が存在することを示せばよい.![]() の第
の第![]() 要素
要素![]() が(12.1)式で与えられるとすると,教科書図4.1より
が(12.1)式で与えられるとすると,教科書図4.1より![]() は入力
は入力![]() ,出力
,出力![]() の1入力1出力システムの伝達関数と考えられる.したがって,
の1入力1出力システムの伝達関数と考えられる.したがって,![]() は定理3.4と教科書(3.49)式により
は定理3.4と教科書(3.49)式により
![\begin{eqnarray*}
A_{ij} &=& \left[ \begin{array}{cccccc}
0 & 1 & 0 & \cdots & \...
...a_1 & \cdots & \cdots & \cdots & \gamma_{k-1} \end{array}\right]
\end{eqnarray*}](img622.png)
![\begin{eqnarray*}
\tilde{A} &=& \left[\begin{array}{cccccccc}
A_{11} & & & & & &...
... & \\
& & & & & & &c_{r1} & \cdots & c_{rm}
\end{array}\right]
\end{eqnarray*}](img623.png)