定理4.4 ある実現が最小実現であるための必要十分条件は,それが可制御かつ可観測なことである.
(証明) 必要性,すなわち最小実現が可制御でないか,可観測でないと仮定する.明らかにこの場合はシステムの状態方程式は正準分解でき,これによってより小さな次元数の可制御可観測なサブシステムが得られる.さらにこのサブシステムは定理4.2により,一つの実現となっている.したがって初めに得られた実現は最小実現であることに矛盾する.
十分性をしめす.このため伝達関数行列![]() に対する可制御可観測な
に対する可制御可観測な![]() 次の実現
次の実現![]() が得られたとし,これが最小実現でないと仮定する.すなわち
が得られたとし,これが最小実現でないと仮定する.すなわち![]() 次の実現
次の実現
![]() が存在すると仮定する.これらのシステムに対し,
が存在すると仮定する.これらのシステムに対し,
![]() の定義式(2.5):
の定義式(2.5):
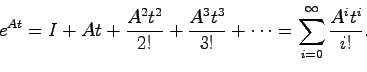
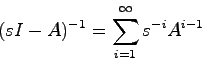
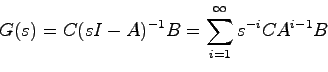
次にハンケル行列と呼ばれる対称行列![]() を次式により定義する:
を次式により定義する:
![\begin{displaymath}
H_\nu = \left[ \begin{array}{ccccc}
J_0 & J_1 & J_2 & \cdots...
...} & J_\nu & J_{\nu+1} & \cdots & J_{2\nu-2}
\end{array}\right]
\end{displaymath}](img637.png)
![\begin{eqnarray*}
H_n &=& \left[ \begin{array}{ccccc}
CB & CAB & CA^2B & \cdots ...
...cc} B & AB & \cdots & A^{n-1}B \end{array}\right]\\
&=& M_O M_C
\end{eqnarray*}](img639.png)
![\begin{eqnarray*}
\bar{H}_n &=& \left[ \begin{array}{ccccc}
\bar{C}\bar{B} & \ba...
...ar{A}\bar{B} & \cdots &
\bar{A}^{n-1}\bar{B} \end{array}\right]
\end{eqnarray*}](img643.png)
定理4.5 与えられた伝達関数行列![]() に対する最小実現は全て同値である.
に対する最小実現は全て同値である.
(証明) ![]() の任意の2つの最小実現(
の任意の2つの最小実現(![]() 次)を
次)を
![]() とすると,前定理の証明からもわかるように,これらのマルコフパラメータ
とすると,前定理の証明からもわかるように,これらのマルコフパラメータ
![]() は一致する.すなわち
は一致する.すなわち
![]() が成り立つ.システム
が成り立つ.システム
![]() の可制御性行列,可観測性行列をそれぞれ
の可制御性行列,可観測性行列をそれぞれ![]() 及び
及び
![]() とすると,ハンケル行列
とすると,ハンケル行列![]() が一致することより
が一致することより
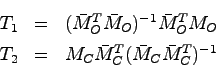
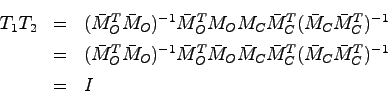
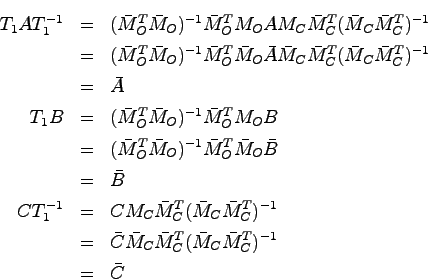
次に最小実現が存在する場合,その次元数を求めることを考える.定理4.4で示したように,最小実現であるための必要十分条件は,それが可制御かつ可観測であることであった.さらに定理4.4の証明から判るように,最小実現のハンケル行列を![]() とすると
とすると
伝達関数行列![]() の各要素の分母の最小公倍多項式を
の各要素の分母の最小公倍多項式を![]() とし,
とし,![]() の次数を
の次数を![]() とする.さらに
とする.さらに
![]() を
を![]() のマクミラン次数と呼ぶ.
のマクミラン次数と呼ぶ.
定理4.6 最小実現の次元数はマクミラン次数に等しい.
(証明)伝達関数行列![]() の最小実現を
の最小実現を![]() とし,その次元数を
とし,その次元数を![]() とし,各係数行列
とし,各係数行列![]() はそれぞれ
はそれぞれ
![]() 行列とする.
システム
行列とする.
システム![]() の
の![]() 次のハンケル行列を
次のハンケル行列を![]() とすると
とすると
![\begin{eqnarray*}
H_m &=& \left[ \begin{array}{c}
M_O CA^n \vdots CA^{m...
...} M_C & C A^{n+m-1} B & \cdots & CA^{2(m-1)}B
\end{array}\right]
\end{eqnarray*}](img670.png)
![\begin{displaymath}
\begin{array}{c}
{\rm rank}\left[ \begin{array}{cccc}
M_C & ...
...B & \cdots & CA^{2(m-1)}B
\end{array}\right] \geq n
\end{array}\end{displaymath}](img672.png)
さて,上記のことを証明するために以下のような準備を行なう.
いま![]() を
を
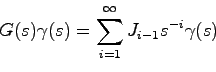
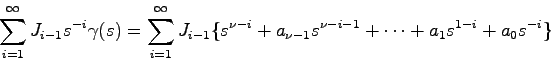
以上の準備から,![]() なる任意の
なる任意の![]() に対し
に対し![]() 次のハンケル行列
次のハンケル行列![]() を求めれば
を求めれば
![\begin{eqnarray*}
H_{k+1} &=& \left[ \begin{array}{cccc}
J_0 & J_1 & \cdots & J_...
...k+1} & \cdots & J_{2k-1}
\end{array} & J_{2k}
\end{array}\right]
\end{eqnarray*}](img688.png)
![\begin{eqnarray*}
H_{k+1} &=& \left[ \begin{array}{cccccc}
I_r \\
& I_r \\
& &...
... & & \vdots \\
& & & & & I_m & -a_{\nu-1}I_m
\end{array}\right]
\end{eqnarray*}](img690.png)
例4.2 伝達関数行列![]() が
が
![\begin{displaymath}
G(s) = \left[ \begin{array}{cc}
\displaystyle{\frac{2}{s+1}}...
...rac{1}{s+1}} & \displaystyle{\frac{1}{s+1}}
\end{array}\right]
\end{displaymath}](img692.png)
まず
![]() であるから
であるから![]() である.またマルコフパラメータ
である.またマルコフパラメータ![]() は
は
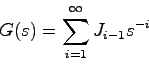
![\begin{eqnarray*}
J_0 &=& \lim_{s \to \infty}sG(s) = \lim_{s \to \infty}
\left[ ...
...ight]=\left[ \begin{array}{cc}
2 & 0 1 & 1 \end{array}\right]
\end{eqnarray*}](img697.png)
![\begin{displaymath}
{\rm rank}H_2 = {\rm rank}\left[ \begin{array}{cc}
J_0 & J_1 J_1 & J_2 \end{array}\right] = 3
\end{displaymath}](img698.png)
システム![]() と同じ伝達関数を持ち,より小さな次元の状態変数によって表現されるシステム
と同じ伝達関数を持ち,より小さな次元の状態変数によって表現されるシステム
![]() が存在するとき,システム
が存在するとき,システム![]() は可約であるといい,可約でないシステムは既約であるということがある.この用語を用いれば,最小実現とは既約な実現であるということになる.またあるシステムが既約であるための必要十分条件は,そのシステムが可制御可観測なことである.
は可約であるといい,可約でないシステムは既約であるということがある.この用語を用いれば,最小実現とは既約な実現であるということになる.またあるシステムが既約であるための必要十分条件は,そのシステムが可制御可観測なことである.